Question

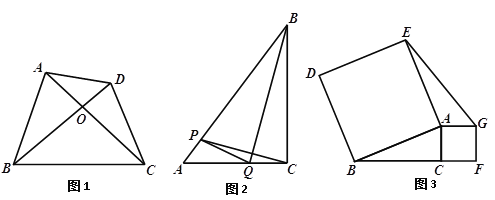
【题目】如图，在矩形ABCD中，E为边AB的中点，将△CBE沿CE翻折得到△CFE，连接AF，若∠EAF=70°，那么∠BCF=______度．

Answer 1

【答案】40

【解析】

由矩形的性质得出∠B=90°，由折叠的性质得出∠EFC=∠B=90°，∠FEC=∠CEB，∠FCE=∠BCE，FE=BE，证出AE=FE，由等腰三角形的性质得出∠EFA=∠EAF=70°，由三角形的外角性质求出∠BEF=∠EAF+∠EFA=140°，得出∠CEB=∠FEC=70°，由直角三角形的性质得出∠FCE=∠BCE=20°，即可得出答案．

∵四边形ABCD是矩形，

∴∠B=90°，

∵E为边AB的中点，

∴AE=BE，

由折叠的性质可得：∠EFC=∠B=90°，∠FEC=∠CEB，∠FCE=∠BCE，FE=BE，

∴AE=FE，

∴∠EFA=∠EAF=70°，

∴∠BEF=∠EAF+∠EFA=140°，

∴∠CEB=∠FEC=70°，

∴∠FCE=∠BCE=90°-70°=20°，

∴∠BCF=20°+20°=40°；

故答案为：40．