题目内容
【题目】如图,已知 ![]() 是⊙
是⊙ ![]() 的直径,
的直径, ![]() 是⊙
是⊙ ![]() 上一点,∠
上一点,∠ ![]() 的平分线交⊙
的平分线交⊙ ![]() 于点
于点 ![]() ,交⊙
,交⊙ ![]() 的切线
的切线 ![]() 于点
于点 ![]() ,过点
,过点 ![]() 作
作 ![]() ⊥
⊥ ![]() ,交
,交 ![]() 的延长线于点
的延长线于点 ![]() .
.
(1)求证: ![]() 是⊙
是⊙ ![]() 的切线;
的切线;
(2)若 ![]() .求
.求 ![]() 值.
值.
【答案】
(1)证明:如图,连结OD,
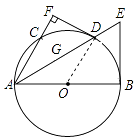
∵AD平分∠BAC,
∴∠DAF=∠DAO,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠DAF=∠ODA,
∴AF∥OD,
∵DF⊥AC,
∴OD⊥DF,
∴DF是⊙O的切线,
(2)解:①连接BD,
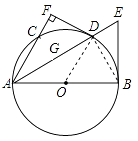
∵直径AB,∴∠ADB=90°,∵圆O与BE相切,∴∠ABE=90°,∵∠DAB+∠DBA=∠DBA+∠DBE=90°,∴∠DAB=∠DBE,∴∠DBE=∠FAD,∵∠BDE=∠AFD=90°,∴△BDE∽△AFD,∴ ![]()
②连接OC,交AD于G,

由①,设BE=2x,则AD=3x,
∵△BDE∽△ABE,
∴ ![]() ,
,
∴ ![]() ,
,
解得:x1=2,x2=- ![]() (不合题意,舍去),
(不合题意,舍去),
∴AD=3x=6,BE=2x=4,AE=AD+DE=8,
∴sin∠EAB= ![]() ,
,
∴∠EAB=30°,
∴∠FAB=60°
【解析】(1)由AD平分∠BAC和OA=OD,得到∠DAF=∠ODA,根据内错角相等两直线平行,得到AF∥OD,由DF⊥AC,得到DF是⊙O的切线;(2)由直径AB,得到∠ADB=90°,由BE是圆O的切线和同角的余角相等,得到∠DAB=∠DBE,∠DBE=∠FAD,根据两角对应相等两三角形相似,得到△BDE∽△AFD,得到比例,求出比值.

练习册系列答案
相关题目