题目内容
【题目】已知:△ABC,点M是平面上一点,射线BM与直线AC交于点D,射线CM与直线AB交于点E.过点A作AF∥CE,AF与BC所在的直线交于点F.

(1)如图1,当BD⊥AC,CE⊥AB时,写出∠BAD的一个余角,并证明∠ABD=∠CAF;
(2)若∠BAC=80°,∠BMC=120°.
①如图2,当点M在△ABC内部时,用等式表示∠ABD与∠CAF之间的数量关系,并加以证明;
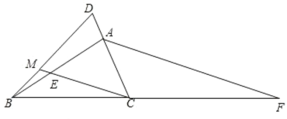
②如图3,当点M在△ABC外部时,依题意补全图形,并直接写出用等式表示的∠ABD与∠CAF之间的数量关系.
【答案】(1)∠ABD等(答案不唯一),证明见解析;(2)①∠ABD+∠CAF=40°,证明见解析;
②∠CAF-∠ABD= 40°.
【解析】
(1)根据余角的定义写出即可;根据同角的余角相等得到∠ABD=∠ACE,再由平行线的性质得到∠ACE=∠CAF,从而得出结论;
(2) ①由∠BMC是△MDC的外角可得∠BMC=∠MDC+∠MCD,又∠MDC是△ABD的外角可得∠MDC=∠BAC+∠ABD,根据平行线的性质可得∠MCD=∠CAF,则证得∠BMC=∠BAC+∠ABD+∠CAF,代入数值计算即可得出结论;
②方法同①.
(1)∵BD⊥AC,CE⊥AB,
∴∠ABD+∠BAC= 90° , ∠ACE+∠BAC= 90° ,
∴∠ABD=∠ACE,
又∵AF∥CE,
∴∠ACE=∠CAF,
∴∠ABD=∠CAF.
(2)①∠ABD+∠CAF=40°,理由为:
∵∠BMC是△MDC的外角
∴∠BMC=∠MDC+∠MCD,
∵∠MDC是△ABD的外角,
∴∠MDC=∠BAC+∠ABD,
∵AF∥CE,
∴∠MCD=∠CAF,
∴∠BMC=∠BAC+∠ABD+∠CAF,
∵∠BAC=80°,∠BMC=120°,
∴120°=80°+∠ABD+∠CAF,
∴∠ABD+∠CAF=40°.
②补全图形见下图,∠CAF-∠ABD= 40°
∵∠BEC是△AEC的外角
∴∠BEC=∠BAC+∠ACE,
∵∠BEC是△BME的外角,
∴∠BEC=∠BME+∠ABD,
∴∠BAC+∠ACE=∠BME+∠ABD,
∵AF∥CE,
∴∠ACE=∠CAF,
∴∠BAC+∠CAF=∠BMC+∠ABD,
∵∠BAC=80°,∠BMC=120°,
∴80°+∠CAF=120°+∠ABD,
∴∠CAF-∠ABD= 40°

【题目】日前,中国儿童文学作家曹文轩荣获2016年国际儿童读物联盟(IBBY)国际安徒生奖,新安书店抓住契机,以每本20元的价格购进一批畅销书《曹文轩作品集》.销售过程中发现,每月销售量y(本)与销售单价x(元)之间的关系如下表所示,按照表中y与x的关系规律,解决下面的问题:
x | 25 | 28 | 30 | 32 | 35 |
y | 250 | 220 | 200 | 180 | 150 |
(1)试求出y与x的函数关系式.
(2)销售单价在什么范围时,书店能盈利?
(3)如果想要每月获得的利润不低于2000元,那么该书店每月的成本最少需要多少元?(成本=每本进价×销售量)

