题目内容
如图,在△ABC中,∠B=40°,△ABC的两个外角的平分线交于E点,求∠AEC的度数.
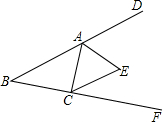

∵AE,CE是△ABC的两个外角的平分线,
∴∠ACE=
(∠B+∠BAC),∠CAE=
(∠B+∠BCA),
∵∠BCA+∠BAC=180°-∠B,
∴∠AEC=180°-∠ACE-∠CAE
=180°-
(∠B+∠BAC+∠B+∠BCA)
=180°-
(2∠B+180°-∠B)
=90°-
∠B.
=70°.
∴∠ACE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BCA+∠BAC=180°-∠B,
∴∠AEC=180°-∠ACE-∠CAE
=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=90°-
| 1 |
| 2 |
=70°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目