题目内容
【题目】如图1,P 为△ABC 内一点,连接 PA、PB、PC,在△PAB、△PBC 和△PAC 中,如果存在一个三角形与△ABC 相似,那么就称 P 为△ABC 的自相似点.
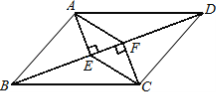
(1)如图 2,已知 Rt△ABC 中,∠ACB=90°,CD 是 AB 上的中线,过点 B 作 BE⊥CD,垂足为 E,试说明 E 是△ABC 的自相似点.
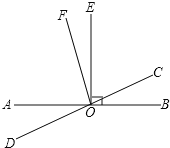
(2)如图 3,在△ABC 中,∠A<∠B<∠C.若△ABC 的三个内角平分线的交 点 P 是该 三角形的自相似点,求该三角形三个内角的度数.

【答案】(1)详见解析;(2)![]()
【解析】
(1)根据已知条件得出∠BEC=∠ACB,以及∠BCE=∠ABC,得出△BCE∽△ABC,即可得出结论;
(2)根据∠PBC=∠A,∠BCP=∠ABC=∠2∠PBC=2∠A,∠ACB=2∠BCP=4∠A,即可得出各内角的度数.
解:(1)在Rt△ABC中,∠ACB=90°,CD是AB上的中线,
∴CD=![]() AB,
AB,
∴CD=BD,
∴∠BCE=∠ABC,
∵BE⊥CD,∴∠BEC=90°,
∴∠BEC=∠ACB,
∴△BCE∽△ABC,
∴E是△ABC的自相似点;
(2)∵P是△ABC的内心,∴∠PBC=![]() ∠ABC,∠PCB=
∠ABC,∠PCB=![]() ∠ACB,
∠ACB,
∵△ABC的内心P是该三角形的自相似点,
∴△BCP∽△ABC
∴∠PBC=∠A,∠BCP=∠ABC=2∠PBC=2∠A,∠ACB=2∠BCP=4∠A,
∴∠A+2∠A+4∠A=180°,
∴∠A=![]() ,
,
∴该三角形三个内角度数为:![]() ,
,![]() ,
,![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目