题目内容
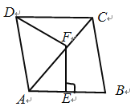
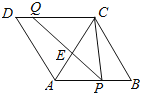
【题目】如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点为A′,当CA′的长度最小时,CQ的长为_____.
【答案】7
【解析】
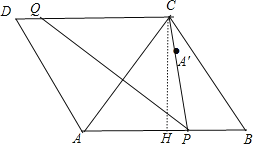
作CH⊥AB于H,如图,根据菱形的性质可判断△ABC为等边三角形,则CH=![]() AB=4
AB=4![]() ,AH=BH=4,再利用勾股定理计算出CP=7,再根据折叠的性质得点A′在以P点为圆心,PA为半径的弧上,利用点与圆的位置关系得到当点A′在PC上时,CA′的值最小,然后证明CQ=CP即可.
,AH=BH=4,再利用勾股定理计算出CP=7,再根据折叠的性质得点A′在以P点为圆心,PA为半径的弧上,利用点与圆的位置关系得到当点A′在PC上时,CA′的值最小,然后证明CQ=CP即可.
作CH⊥AB于H,如图,
∵菱形ABCD的边AB=8,∠B=60°,
∴△ABC为等边三角形,
∴CH=![]() AB=4
AB=4![]() ,AH=BH=4,
,AH=BH=4,
∵PB=3,
∴HP=1,
在Rt△CHP中,CP=![]() =7,
=7,
∵梯形APQD沿直线PQ折叠,A的对应点A′,
∴点A′在以P点为圆心,PA为半径的弧上,
∴当点A′在PC上时,CA′的值最小,
∴∠APQ=∠CPQ,而CD∥AB,
∴∠APQ=∠CQP,
∴∠CQP=∠CPQ,
∴CQ=CP=7.
故答案为:7.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目