题目内容
【题目】等腰![]() 中,
中,![]() ,作
,作![]() 的外接圆⊙O.
的外接圆⊙O.
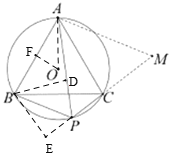
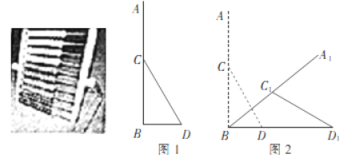
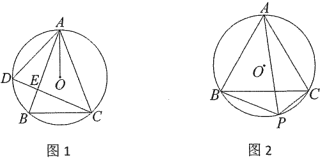
(1)如图1,点![]() 为
为![]() 上一点(不与A、B重合),连接AD、CD、AO,记
上一点(不与A、B重合),连接AD、CD、AO,记![]() 与
与![]() 的交点为
的交点为![]() .
.
①设![]() ,若
,若![]() ,请用含
,请用含![]() 与
与![]() 的式子表示
的式子表示![]() ;
;
②当![]() 时,若
时,若![]() ,求
,求![]() 的长;
的长;
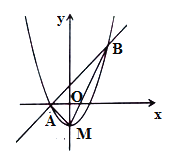
(2)如图2,点![]() 为
为![]() 上一点(不与B、C重合),当BC=AB,AP=8时,设
上一点(不与B、C重合),当BC=AB,AP=8时,设![]() ,求
,求![]() 为何值时,
为何值时,![]() 有最大值?并请直接写出此时⊙O的半径.
有最大值?并请直接写出此时⊙O的半径.
【答案】(1)①![]() ;②
;②![]() ;(2)PB=5时,S有最大值,此时⊙O的半径是
;(2)PB=5时,S有最大值,此时⊙O的半径是![]() .
.
【解析】
(1)①连接BO、CO,利用SSS可证明△ABO≌△ACO,可得∠BAO=∠CAO=y,利用等腰三角形的性质及三角形内角和定理可用y表示出∠ABC,由圆周角定理可得∠DCB=∠DAB=x,根据![]() 即可得答案;
即可得答案;
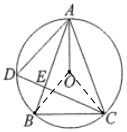
②过点![]() 作
作![]() 于点
于点![]() ,根据垂径定理可得AF的长,利用勾股定理可求出OF的长,由(1)可得
,根据垂径定理可得AF的长,利用勾股定理可求出OF的长,由(1)可得![]() ,由AB⊥CD可得n=90°,即可证明y=x,根据AB⊥CD,OF⊥AC可证明△AED∽△AFO,设DE=a,根据相似三角形的性质可
,由AB⊥CD可得n=90°,即可证明y=x,根据AB⊥CD,OF⊥AC可证明△AED∽△AFO,设DE=a,根据相似三角形的性质可![]() ,由∠D=∠B,∠AED=∠CEB=90°可证明△AED∽△CEB,设
,由∠D=∠B,∠AED=∠CEB=90°可证明△AED∽△CEB,设![]() ,根据相似三角形的性质可得
,根据相似三角形的性质可得![]() ,根据线段的和差关系和勾股定理列方程组可求出a、b的值,根据△AED∽△AFO即可求出AD的值;
,根据线段的和差关系和勾股定理列方程组可求出a、b的值,根据△AED∽△AFO即可求出AD的值;
(2)延长![]() 到
到![]() ,使得
,使得![]() ,过点B作BD⊥AP于D,BE⊥CP,交CP延长线于E,连接OA,作OF⊥AB于F,根据BC=AB可得三角形ABC是等边三角形,根据圆周角定理可得∠APM=60°,即可证明△APM是等边三角形,利用角的和差关系可得∠BAP=∠CAM,利用SAS可证明△BAP≌△CPM,可得BP=CM,即可得出PB+PC=AP,设
,过点B作BD⊥AP于D,BE⊥CP,交CP延长线于E,连接OA,作OF⊥AB于F,根据BC=AB可得三角形ABC是等边三角形,根据圆周角定理可得∠APM=60°,即可证明△APM是等边三角形,利用角的和差关系可得∠BAP=∠CAM,利用SAS可证明△BAP≌△CPM,可得BP=CM,即可得出PB+PC=AP,设![]() ,则
,则![]() ,利用∠APB和∠BPE的正弦可用x表示出BD、BE的长,根据
,利用∠APB和∠BPE的正弦可用x表示出BD、BE的长,根据![]() 可得S与x的关系式,根据二次函数的性质即可求出S取最大值时x的值,利用∠BPA的余弦及勾股定理可求出AB的长,根据等边三角形的性质及垂径定理求出OA的长即可得答案.
可得S与x的关系式,根据二次函数的性质即可求出S取最大值时x的值,利用∠BPA的余弦及勾股定理可求出AB的长,根据等边三角形的性质及垂径定理求出OA的长即可得答案.
(1)①连接BO,CO,
∵![]() ,且
,且![]() 为公共边,
为公共边,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,
,
∵![]() ,
,
∴![]()
∴![]() .
.
②过点![]() 作
作![]() 于点
于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴△AED∽△AFO,
∴![]() =,即
=,即![]() ,
,
设![]() ,则
,则![]()
∵![]() ,
,
∴△AED∽△CEB,
∴![]() ,即
,即![]()
设![]() ,则
,则![]() ,
,
∴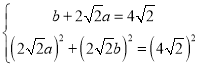
解得:![]() 或
或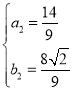 ,
,
∵a>0,b>0,
∴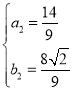 ,即DE=
,即DE=![]() ,
,
∵△AED∽△AFO,
∴![]() ,
,
∴AD=![]() =3
=3![]() =
=![]() .
.
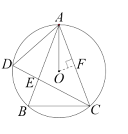
(2)延长![]() 到
到![]() ,使得
,使得![]() ,过点B作BD⊥AP于D,BE⊥CP,交CP延长线于E,连接OA,作OF⊥AB于F,
,过点B作BD⊥AP于D,BE⊥CP,交CP延长线于E,连接OA,作OF⊥AB于F,
∵BC=AB,AB=AC,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵∠BAP+∠PAC=∠CAM+∠PAC=60°,
∴![]()
在△BAP和△CAM中,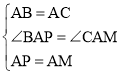 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
设![]() ,则
,则![]() ,
,
∵∠APB=∠ACB=60°,∠APM=60°,
∴∠BPE=60°,
∴BE=PB·sin60°=![]() ,PD=PB·sin60°=
,PD=PB·sin60°=![]() ,
,
∵![]() ,
,
∴S=![]() PC·BE+
PC·BE+![]() ×
×![]() AP·BD=
AP·BD=![]() ,
,
∴当![]() 时,即PB=5时,S有最大值,
时,即PB=5时,S有最大值,
∴BD=![]() =
=![]() ,PD=PB·cos60°=
,PD=PB·cos60°=![]() ,
,
∴AD=AP-PD=![]() ,
,
∴AB=![]() =7,
=7,
∵△ABC是等边三角形,O为△ABC的外接圆圆心,
∴∠OAF=30°,AF=![]() AB=
AB=![]() ,
,
∴OA=![]() =
=![]() .
.
∴此时![]() 的半径是
的半径是![]() .
.