题目内容
【题目】如图所示,已知直线MN//PQ,直线AC交MN、PQ于点A、C,所得的同旁内角的平分线AB、BC和AD、CD分别相交于点B、D.试猜想AC与BD的关系,并说明理由.
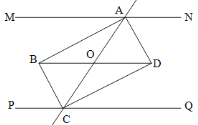
【答案】AC与BD相等且互相平分,理由见解析.
【解析】
已知MN//PQ,可得∠MAC+∠ACP=180°,已知AB、CB分别平分∠MAC、∠ACP,即∠BAC=![]() ∠MAC,∠BCA=
∠MAC,∠BCA=![]() ∠ACP,得到∠BAC+∠BCA=90°,∠ABC=90°,同理可得∠ADC=90°,根据角平分线的性质可得到∠ACB+∠ACD=90°,即∠BCD=90°,证得四边形ABCD是矩形,得到AC与BD相等且互相平分.
∠ACP,得到∠BAC+∠BCA=90°,∠ABC=90°,同理可得∠ADC=90°,根据角平分线的性质可得到∠ACB+∠ACD=90°,即∠BCD=90°,证得四边形ABCD是矩形,得到AC与BD相等且互相平分.
AC与BD相等且互相平分,理由如下:
∵MN//PQ,
∴ ∠MAC+∠ACP=180°
又∵AB、CB分别平分∠MAC、∠ACP
∴∠BAC=![]() ∠MAC,∠BCA=
∠MAC,∠BCA=![]() ∠ACP
∠ACP
∴∠BAC+∠BCA=90°
∴∠ABC=90°
同理可得∠ADC=90°
又∠ACP+∠ACQ=180°,CB、CD分别平分∠ACP、∠ACQ
∴∠ACB+∠ACD=90°
即∠BCD=90°
∴四边形ABCD是矩形
∴AC与BD相等且互相平分

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
【题目】某企业新增了一个化工项目,为了节约资源,保护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情况如下表:
A型 | B型 | |
价格(万元/台) | 12 | 10 |
月污水处理能力(吨/月) | 200 | 160 |
经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.
(1)该企业有几种购买方案?
(2)哪种方案更省钱,说明理由.