题目内容
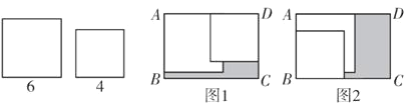
【题目】如图，已知在矩形ABCD内，将两张边长分别为6和4的正方形纸片按图1，图2两种方式放置(图1，图2中两张正方形纸片均有部分重叠)，矩形中末被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为S1，图2中阴影部分的面积为S2.当AD-AB=2时，S2-S1的值为________.
【答案】8
【解析】
利用正方形的性质及矩形的性质，设AD=x，AB=y，分别用含x、y的代数式表示出S2和S1 ， 再求出S2-S1 ， 再整体代入即可求解.
解：设AD=x，AB=y，
由题意得:
S1=xy-4x-12，S2=xy-4y-12，
∴S2-S1=xy-4y-12-(xy-4x-12)=-4y+4x=4（x-y）
∵AD-AB=2，即x-y=2
∴S2-S1=4×2=8.
故答案为：8.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
