题目内容
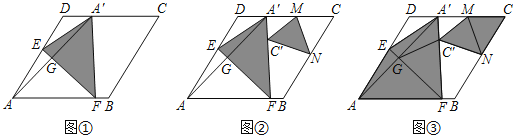
【题目】如图,在一块正方形ABCD木板上要贴三种不同的墙纸,正方形EFCG部分贴A型墙纸,△ABE部分贴B型墙纸,其余部分贴C型墙纸.A型、B型、C型三种墙纸的单价分别为每平方米60元、80元、40元.
探究1:如果木板边长为1米,FC=![]() 米,则一块木板用墙纸的费用需 元;
米,则一块木板用墙纸的费用需 元;
探究2:如果木板边长为2米,正方形EFCG的边长为x米,一块木板需用墙纸的费用为y元,

(1)用含x的代数式表示y(写过程).
(2)如果一块木板需用墙纸的费用为225元,求正方形EFCG的边长为多少米?
【答案】(1)55 y=20x2﹣40x+240(2)正方形EFCG的边长为![]() 或
或![]() 米
米
【解析】解:探究1:∵四边形ABCD是正方形,
∴AB=BC=CD=DA=1,
∴S正方形ABCD=1,
∵四边形EFCG是正方形,
∴EF=CF=![]() ,
,
∴S正方形EFCG=![]() ,BF=
,BF=![]() ,
,
∴S△ABE=![]() =
=![]()
∴空白部分的面积为:1﹣![]() ﹣
﹣![]() =
=![]() ,
,
∴这块木板用墙纸的费用为:![]() +
+![]() 80+40×
80+40×![]() =55元.
=55元.
故答案为:55.
探究2:(1)∵木板边长为2米,
∴木板的面积为:4平方米.
∵正方形EFCG的边长为x米,
∴S正方形EFCG=x2,S△ABE=2﹣x,
∴空白的面积为:4﹣x2﹣(2﹣x)=2﹣x2+x,
y=60x2+80(2﹣x)+40(2﹣x2+x),
y=20x2﹣40x+240.
(2)当y=225时,
225=20x2﹣40x+240,解得:
x1=![]() ,x2=
,x2=![]()
∴正方形EFCG的边长为![]() 或
或![]() 米.
米.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目