Question

【题目】已知：如图，在梯形ABCD中，AD∥BC，∠B=90°，AB=14cm，AD=18cm，BC=21cm，点P从点A开始沿AD边向点D以1cm/秒的速度移动，点Q从点C开始沿CB边向点B以2cm/秒的速度移动．如果P、Q分别从A、C同时出发．设移动的时间为t．

求：（1）t为何值时，梯形PQCD是等腰梯形；

（2）t为何值时，AB的中点E到线段PQ的距离为7cm．

Answer 1

【答案】(1)8秒；（2）t＝3.5或t=7

【解析】试题分析：（1）过P作PN⊥BC于N，过D作DM⊥BC于M，先证明四边形ABMD是矩形，从而得到AD=BM，再根据边与边之间的关系，列一元一次方程3t﹣21=3，得到t=8，即t=8秒时，梯形PQCD是等腰梯形；

（2）在Rt△PQM中，表示出PM=14，QM=3t﹣1，然后根据PM2+QM2=PQ2，得到142+（3t﹣21）2=（21﹣t）2，求得t值即可．

试题解析：

如图1，过P作PN⊥BC于N，过D作DM⊥BC于M，

∵AD∥BC，∠B=90°，DM⊥BC，

∴四边形ABMD是矩形，AD=BM．

∴MC=BC﹣BM=BC﹣AD=3．

又∵QN=BN﹣BQ=AP﹣BQ=t﹣（21﹣2t）=3t﹣21．

若梯形PQCD为等腰梯形，则QN=MC=3．

得3t﹣21=3，t=8，

即t=8秒时，梯形PQCD是等腰梯形．

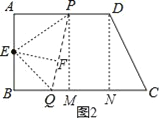
（2）如图2，过E作EF⊥PQ于F，连接PE，EQ，当EF=7cm时，

∵AE=BE=AB=×14=7cm，

∴AE=EF=BE，

∵AD∥BC，∠B=90°，

∴∠A=90°，

∵PE=PE，EQ=EQ，

∴△AEP≌△FEP，△BEQ≌△FEQ，

∴PA=PF=t，BQ=FQ=21﹣2t，

∴PQ=PF+FQ=21﹣t，

在Rt△PQM中，PM=14，QM=3t﹣1，

∵PM2+QM2=PQ2，

∴142+（3t﹣21）2=（21﹣t）2，

解得：t=3.5或t=7，

∴当t为3.5或7时，AB的中点E到线段PQ的距离为7cm．