题目内容
【题目】已知：在平面直角坐标系中，等腰Rt△ABC的顶点A、C在坐标轴上运动，且∠ACB=90°，AC=BC．
(1)如图1，当A(0，-2)，C(1，0)，点B在第四象限时，则点B的坐标为_____；
(2)如图2，当点C在x轴正半轴上运动，点A在y轴正半轴上运动，点B在第四象限时，作BD⊥y轴于点D，试判断
与
哪一个是定值，并说明定值是多少？请证明你的结论．
(3)如图3，当点C在y轴正半轴上运动，点A在x轴正半轴上运动，使点D恰为BC的中点，连接DE，求证：∠ADC=∠BDE．
【答案】(3，-1)
【解析】试题分析
（1）如下图1，过点B作BD⊥x轴于点D，结合已知条件证△OAC≌△DCB，就可求得BD和OD的长，从而可得点B的坐标；
（2）如下图2，过点B作BE⊥x轴于点E，结合已知条件可证得△OAC≌△ECB，四边形ODBE是矩形，这样就可得到：CE=OA，BD=OE，所以OC-BD=OC-OE=CE，从而可得： 
；
（3）如下图3，过点B作BG⊥BC于点B，交y轴于点G，结合已知条件可证△CBG≌△ACD，从而可得：∠ADC=∠CGB，BG=CD，结合CD=BD可得BD=BG；再证∠DBE=∠GBE=45°，就可结合BE=BE，证得△DBE≌△GBE，从而可得∠BDE=∠BGE，结合∠ADC=∠CGB就可证得：∠ADC=∠BDE．
试题解析：
(1)∵点A的坐标为：(0，-2)，点C的坐标为：(1，0)，
∴OA=2，OC=1，
作BD⊥CD，
∵∠OCA+∠DCB=90°，∠OAC+∠DCB=90°，
∴∠OAC=∠DCB，
∵在△OAC和△DCB中，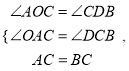 
∴△OAC≌△DCB，(AAS)
∴CD=OA=2，BD=OC=1，OD=3，
∴B点坐标为(3，-1)；
(2)作BE⊥OC，则四边形ODBE为矩形，
∵∠ACO+∠BCO=90°，∠ACO+∠OAC=90°，
∴∠BCO=∠CAO，
∵△OAC和△ECB中， 
∴△OAC≌△ECB，(AAS)
∴EC=OA，
∵四边形ODBE为矩形，
∴OE=BD，
∵OC=OE+EC，
∴OC=AO+BD，
∴OC-BD=OA，
∴
，即
是定值，且定值为1；
(3)过点B作BG⊥BC交y轴于点G，
∴∠CBG=∠ACD=90°，
∵∠BCG+∠ACG=90°，∠ACO+∠DCO=90°，
∴∠DCO=∠CAO．
在△BCG和△CAD中，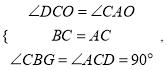 
∴△BCG≌△CAD(ASA)，
∴BG=CD=BD，∠BGE=∠ADC，
∵在Rt△ABC中，∠ACB=90°，AC=BC，
∴∠ABC=∠BAC=45°，
又∵∠CBG=90°，
∴∠EBG=∠DBE=45°，
在△DBE和△GBE中，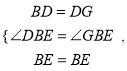 
∴△DBE≌△GBE(SAS)，
∴∠BDE=∠BGE，
由∵∠BGE=∠ADC，
∴∠ADC=∠BDE．
