题目内容
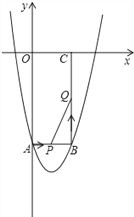
【题目】(12分)如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.
(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时,设△PBQ的面积为S,试写出S与t之间的函数关系式,并写出t的取值范围.
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
【答案】(1)y=![]() x2-4x-12;(2)①S=-t2+6t,0<t<6;②抛物线上存在点R(3,-18),使P、B、Q、R为顶点的四边形是平行四边形.
x2-4x-12;(2)①S=-t2+6t,0<t<6;②抛物线上存在点R(3,-18),使P、B、Q、R为顶点的四边形是平行四边形.
【解析】试题分析:(1)根据矩形的对边相等求出点A、B的坐标,把两点的坐标代入抛物线解析式,再联立18a+c=0,解关于a、b、c的三元一次方程组,然后即可得到抛物线的关系式;
(2)①根据速度的不同,表示出BP、BQ的长度,然后利用三角形的面积公式列式整理即可得到S与t的关系式,根据速度分别求出点P与点Q的运动时间即可得到t取值范围;
②先根据二次函数的最大值问题求出S取最大值时的t的值,从而求出点P与点Q的坐标,再根据平行四边形的对边平行且相等,分QR与PB是对边时,PR与QB是对边时,两种情况求出点Q的坐标,然后代入抛物线解析式进行验证,如果点Q在抛物线上,则存在,否则不存在.
试题解析:(1)∵矩形OABC边长OA、OC分别为12cm和6cm,
∴点A、B的坐标分别为A(0,-12),B(6,-12),
又∵抛物线y=ax2+bx+c经过点A、B,且18a+c=0,
∴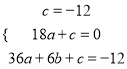 ,
,
解得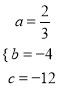 ,
,
∴抛物线解析式为y=![]() x2-4x-12;
x2-4x-12;
(2)①根据题意,PB=AB-AP=6-t,BQ=2t,
所以,S=![]() PBBQ=
PBBQ=![]() (6-t)×2t=-t2+6t,
(6-t)×2t=-t2+6t,
即S=-t2+6t,
点P运动的时间为6÷1=6秒,
点Q运动的时间为12÷2=6秒,
所以,t的取值范围是0<t<6;
②抛物线上存在点R(3,-18),使P、B、Q、R为顶点的四边形是平行四边形.
理由如下:∵S=-t2+6t=-(t-3)2+9,
∴当t=3秒时,S取最大值,
此时,PB=AB-AP=6-t=6-3=3,
BQ=2t=2×3=6,
所以,要使P、B、Q、R为顶点的四边形是平行四边形,
(i)当QR与PB是对边时,点R的横坐标是6+3=9,纵坐标是-(12-6)=-6,
所以点R的坐标为(9,-6),
此时![]() ×92-4×9-12=6≠-6,
×92-4×9-12=6≠-6,
所以点R不在抛物线上,
(ii)当PR与QB是对边时,点R的横坐标是3,纵坐标是-(12+6)=-18,
所以点R的坐标是(3,-18),
此时, ![]() ×32-4×3-12=-18,
×32-4×3-12=-18,
所以点R在抛物线上,
综上所述,抛物线上存在点R(3,-18),使P、B、Q、R为顶点的四边形是平行四边形.