Question

【题目】如图，正方形的面积为，点是边上一点，，将线段绕点旋转，使点落在直线上，落点记为，则________，的长为________．

Answer 1

【答案】

【解析】

当点F在线段BC上时，由旋转的性质可得△ADE≌△ABF，可得到BF=DE，∠DAE=∠BAF=30°，可求得答案；当点F在线段CB的延长线上时，可证得△ABF≌△ADE，则可求得∠EAF=90°，此时FC=BF+BC，可求得答案．

∵四边形ABCD为正方形，且面积为3

∴∠D=∠B=∠BAD=90°，AD=AB=BC=CD=，且AE=AF，

①当F在线段BC上时，如图1，

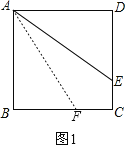
在Rt△ADE和Rt△ABF中，

，

∴Rt△ADE≌Rt△ABF（HL），

∴∠DAE=∠BAF，BF=DE=1，

又∵在Rt△ADE中，DE=1，AD=，

∴tan∠DAE=，

∴∠BAF=∠DAE=30°，

∴∠EAF=90°-30°-30°=30°，FC=BC-BF=-1；

②当点F在线段CB的延长线上时，如图2，

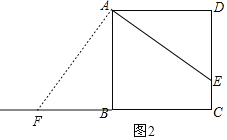
则可证得△ABF≌△ADE，

∴∠EAB=∠DAE，

∴∠EAF=∠FAB+∠BAE=∠BAE+∠DAE=90°，FC=FB+BC=+1；

故答案为：30°或90°；-1或+1．