题目内容
【题目】如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G、F两点.
(1)求证:AB与⊙O相切;
(2)若等边三角形ABC的边长是4,求线段BF的长?
【答案】
(1)
证明:过点O作OM⊥AB,垂足是M.
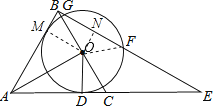
∵⊙O与AC相切于点D.
∴OD⊥AC,
∴∠ADO=∠AMO=90°.
∵△ABC是等边三角形,
∴∠DAO=∠NAO,
∴OM=OD.
∴AB与⊙O相切;
(2)
解:过点O作ON⊥BE,垂足是N,连接OF.
∵O是BC的中点,
∴OB=2.
在直角△OBM中,∠MBO=60°,
∴OM=OBsin60°=![]() ,BM=OBcos60°=1.
,BM=OBcos60°=1.
∵BE⊥AB,
∴四边形OMBN是矩形.
∴ON=BM=1,BN=OM=![]() .
.
∵OF=OM=![]() ,
,
由勾股定理得NF=![]() .
.
∴BF=BN+NF=![]() +
+![]() .
.
【解析】(1)过点O作OM⊥AB,垂足是M,证明OM等于圆的半径OD即可;
(2)过点O作ON⊥BE,垂足是N,连接OF,则四边形OMBN是矩形,在直角△OBM利用三角函数求得OM和BM的长,则BN和ON即可求得,在直角△ONF中利用勾股定理求得NF,则BF即可求解.

【题目】某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
(1)根据题意,填写下表:
蔬菜的批发量(千克) | … | 25 | 60 | 75 | 90 | … |
所付的金额(元) | … | 125 |
| 300 |
| … |
(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出y与x之间的函数关系式;
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?






