题目内容
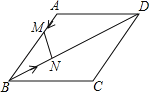
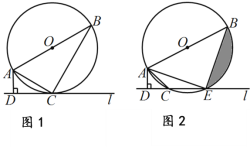
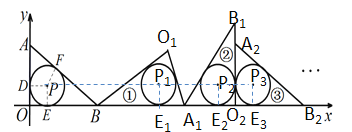
【题目】如图,将一张画有内切圆⊙P的直角三角形纸片AOB置于平面直角坐标系中,已知点A(0,3),B(4,0),⊙P与三角形各边相切的切点分别为D、E、F. 将直角三角形纸片绕其右下角的顶点依次按顺时针方向旋转,第一次旋转至图①位置,第二次旋转至图②位置,…,则直角三角形纸片旋转2018次后,它的内切圆圆心P的坐标为____.

【答案】(8075,1)
【解析】
旋转后的三角形内切圆的圆心分别为P1,P2,P3,过圆心作垂直于x轴,分别交x轴于点为E1,E2,E3,根据已知A(0,3),B(4,0),可求得AB长度和三角形内切圆的半径,依次求出OE1,OE2,OE3,OE4,OE5,OE6的长,找到规律,求得OE2018的长,即可求得直角三角形纸片旋转2018次后,它的内切圆圆心P的坐标.
如图所示,旋转后的三角形内切圆的圆心分别为P1,P2,P3,过圆心作垂直于x轴,分别交x轴于点为E1,E2,E3
设三角形内切圆的半径为r
∵△AOB是直角三角形,A(0,3),B(4,0)
∴![]()
∵⊙P是△AOB的内切圆
∴![]()
即![]()
∴r=1
∴BE=BF=OB-OE=4-1=3
∵△BO1A1是△AOB绕其B点按顺时针方向旋转得到
∴BE1=BF=3
∴OE1=4+3
∵A1E2=3-1=2
∴OE2=4+5+2
∴OE3=4+5+3+1
同理可推得OE4=4+5+3+4+3,OE5=4+5+3+4+5+2,OE6=4+5+3+4+5+3+1
2018÷3=672![]() 2
2
OE2018=672×(4+5+3)+(4+5+2)=8075
三角形在翻折后内切圆的纵坐标不变
∴P2018(8075,1)
故答案为:(8075,1)

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】表中所列![]() 、
、![]() 的7对值是二次函数
的7对值是二次函数![]() 图象上的点所对应的坐标,其中
图象上的点所对应的坐标,其中![]()
| … |
|
|
|
|
|
|
| … |
| … | 6 |
| 11 |
| 11 |
| 6 | … |
根据表中提供约信息,有以下4个判断:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 的值是
的值是![]() ;④
;④![]() ;其中判断正确的是( )
;其中判断正确的是( )
A.①②③B.①②④C.①③④D.②③④