题目内容
【题目】如图是某月的日历表,在此目历表上可以用一个“十”字圈出5个数.
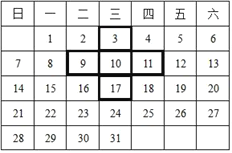
(1)如图中四周的4个数3、9、17、11的和与中间的数10有什么数量关系?
(2)照此方法,任意圈出的5个数是否都具有这样的数量关系?请通过整式的运算说明理由.
(3)用(2)的结论说明圈出的5个数的和能否等于125?
【答案】(1)数3、9、17、11的和与中间的数10是4倍关系;(2)任意圈出的5个数都具有这样的数量关系;(3)圈出的5个数的和不能等于125.
【解析】
(1)计算出四周的4个数的和,与中间的数进行比较即可;(2)设第二行中间数为x,则其他四个数分别为x﹣7,x﹣1,x+1,x+7,计算这四个数的和为4x,是4的倍数,即可得任意圈出的5个数都具有这样的数量关系;(3)根据(2)的方法可列出方程,求出x的值,再根据日历的天数判断即可.
(1)∵3+9+11+17=40,
40÷10=4,
∴数3、9、17、11的和与中间的数10是4倍关系;
(2)任意圈出的5个数都具有这样的数量关系,
设第二行中间数为x,则其他四个数分别为x﹣7,x﹣1,x+1,x+7,
∴x﹣7+x﹣1+x+1+x+7=4x,
∴任意圈出的5个数都具有这样的数量关系;
(3)x+4x=5x=125,
∴x=25,
∵25为中间数,
∴最大数为25+7=32,
∵日历没有32日,
∴圈出的5个数的和不能等于125.

【题目】在一个不透明的袋中有除颜色外其他完全相同的3个球,每次从袋中摸出一个球,记下颜色后放回搅匀再摸,在摸球试验中得到下表中部分数据:
摸球 总次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
摸到黄球的次数 | 14 | 23 | 38 | 52 | 67 | 86 | 97 | 111 | 120 | 136 |
摸到黄球的频率 | 35% | 32% | 33% | 35% | 35% |
(1)请将上表补充完整(结果精确到1%);
(2)制作折线统计图表示摸到黄球的频率的变化情况;
(3)估计从袋中摸出一个球是黄球的概率是多少.