题目内容
【题目】如图，已知AB∥CD.
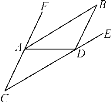
(1)判断∠FAB与∠C的大小关系，请说明理由；
(2)若∠C＝35°，AB是∠FAD的平分线．
①求∠FAD的度数；
②若∠ADB＝110°，求∠BDE的度数．
【答案】(1)∠FAB＝∠C；(2) ①∠FAD＝70°；②∠BDE＝35°
【解析】
（1）相等，根据平行线的性质由AB∥CD，得到∠FAB=∠C即可；
（2）①根据角平分线的定义得到∠FAD=2∠FAB，代入求出即可；
②求出∠ADB+∠FAD=180°，根据平行线的判定得出CF∥BD，再根据平行线的性质推出∠BDE=∠C=35°．
（1）∠FAB与∠C的大小关系是相等，
理由是：∵AB∥CD，
∴∠FAB=∠C．
（2）①∵∠FAB=∠C=35°，
∵AB是∠FAD的平分线，
∴∠FAD=2∠FAB=2×35°=70°，
答：∠FAD的度数是70°．
②∵∠ADB=110°，∠FAD=70°，
∴∠ADB+∠FAD=110°+70°=180°，
∴CF∥BD，
∴∠BDE=∠C=35°，
答：∠BDE的度数是35°．
练习册系列答案
相关题目
