Question

【题目】已知：如图，∠B=∠D=90°，∠A=60°，AB=4，CD=2．求：四边形ABCD的面积．

Answer 1

【答案】解：延长AD，BC，交于点E，

在Rt△ABE中，∠A=60°，AB=4，

∴∠E=30°，AE=2AB=8，

∴BE= =4 ，

在Rt△DCE中，∠E=30°，CD=2，

∴CE=2CD=4，根据勾股定理得：DE= =2 ，

则S四边形ABCD=S△ABE﹣S△DCE= ABBE﹣ DCED=8 ﹣2 =6 ．

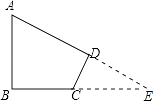
【解析】延长AD，BC，交于点E，在直角三角形ABE中，利用30度角所对的直角边得到AE=2AB，再利用勾股定理求出BE的长，在直角三角形DCE中，同理求出DE的长，四边形ABCD面积=三角形ABE面积﹣三角形DCE面积，求出即可．
【考点精析】关于本题考查的含30度角的直角三角形和勾股定理的概念，需要了解在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案．