题目内容
【题目】已知![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 的切线,
的切线,![]() ,
,![]() 交⊙
交⊙![]() 于点
于点![]() ,
,![]() 是
是![]() 上一点,延长
上一点,延长![]() 交⊙
交⊙![]() 于点
于点![]() .
.
(1)如图①,求![]() 和
和![]() 的大小;
的大小;
(2)如图②,当![]() 时,求
时,求![]() 的大小.
的大小.
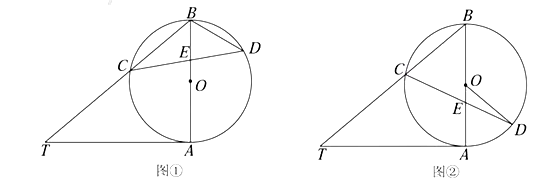
【答案】(1) ∠T=40°,∠CDB=40°;(2)∠CDO =15°.
【解析】
试题分析:(1)如图,连接AC,根据切线的性质定理可得∠TAB=90°,即可求得∠T的度数;根据直径所对的圆周角为直角可得∠ACB=90°,即可求得∠CDO的度数. (2)如图,连接AD,在△BCE中,求得∠BCE=∠BEC=65°,根据圆周角定理的推论可得∠BAD=∠BCD=65°,因OA=OD,根据等腰三角形的性质可得∠ODA=∠OAD=65°,即可得∠CDO=∠ODA-∠ADC=15°.
试题解析:(1)如图,连接AC,
∵![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 的切线,
的切线,
∴AT⊥AB,即∠TAB=90°.
∵![]() ,
,
∴∠T=90°-∠ABT=40°
由![]() 是⊙
是⊙![]() 的直径,得∠ACB=90°,
的直径,得∠ACB=90°,
∴∠CAB=90°-∠ABC=40°
∴∠CDB=∠CAB=40°;
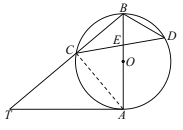
(2)如图,连接AD,
在△BCE中,BE=BC,∠EBC=50°,
∴∠BCE=∠BEC=65°,
∴∠BAD=∠BCD=65°
∵OA=OD
∴∠ODA=∠OAD=65°
∵∠ADC=∠ABC=50°
∴∠CDO=∠ODA-∠ADC=15°.


练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目



