题目内容
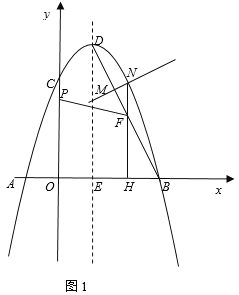
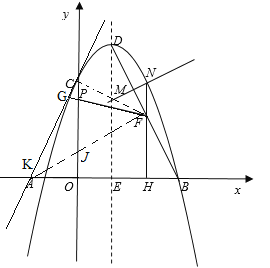
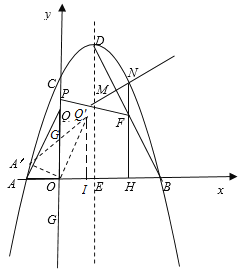
【题目】如图1，在平面直角坐标系中，抛物线y＝ax2－2ax＋3与x轴交于点A，B（点A在点B的左侧），交y轴于点C，点A的坐标为(－1,0)，点D为抛物线的顶点，对称轴与x轴交于点E．
（1）填空：a＝ ，点B的坐标是 ；
（2）连结BD，点M是线段BD上一动点（点M不与端点B，D重合），过点M作MN⊥BD，交抛物线于点N（点N在对称轴的右侧），过点N作NH⊥x轴，垂足为H，交BD于点F，点P是线段OC上一动点，当△MNF的周长取得最大值时，求FP＋
PC的最小值；
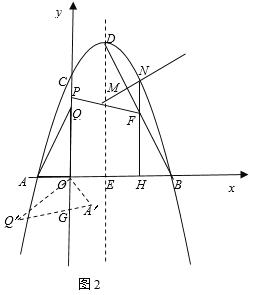
（3）在（2）中，当△MNF的周长取得最大值时，FP＋PC取得最小值时，如图2，把点P向下平移
个单位得到点Q，连结AQ，把△AOQ绕点O顺时针旋转一定的角度α（0°＜α＜360°），得到△A′OQ′，其中边A′Q′交坐标轴于点G．在旋转过程中，是否存在一点G，使得GQ′＝OG？若存在，请直接写出所有满足条件的点Q′的坐标；若不存在，请说明理由．
【答案】（1）
，(3,0)；（2）
；（3）存在，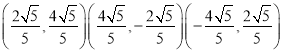
【解析】
（1）将点A的坐标代入抛物线的表达式中可求出a，令y＝0可求出点B的坐标；
（2）通过配方法求出点D的坐标，利用待定系数法求出直线BD的表达式，设点
，
，利用等角的三角函数值相等求出
，利用二次函数的性质可求出使△MNF的周长取得最大值时的m值，在x轴上取点
，过F作CK的垂线段FG交y轴于点P，可得(FP＋
PC )min＝FG，连接FC，FK，FK交y轴与点J，利用
的面积计算求出FG；
（3）由（2）求出点Q的坐标，取AQ的中点G，△AOQ在旋转过程中，只需使AQ的中点G在坐标轴上即可满足GQ′＝OG，分四种情况进行求解．
解：（1）将点A(－1,0) 代入y＝ax2－2ax＋3中得，
，
解得，
，即y＝－x2＋2x＋3，
当y＝0时，－x2＋2x＋3＝0，
解得，
，
，
∴点B的坐标是(3,0)，
故答案为：－1，(3,0)；
（2）∵
，
∴点D(1,4)，点C(0,3)，
设直线BD的表达式为
，且经过点B(3,0)，点D(1,4)，
∴
，
解得，
，
∴
，
设点，，
由图形可知，
，
∵
，
，
∴
，
∴
，
，
，
，
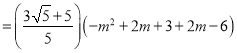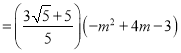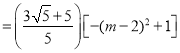∴当m＝2时，C△MNF最大，此时F(2,2)，HF＝2，
在x轴上取点，则∠OCK＝30°，过F作CK的垂线段FG交y轴于点P，此时
，
∴(FP＋PC )min＝(FP＋PG)min＝FG，
连接FC，FK，FK交y轴与点J，
由点，点F(2,2)可求直线FK的表达式为
，
∴点
，
，
，
∴
，即
，
解得，
，
∴当△MNF的周长取得最大值时，FP＋PC的最小值为；
（3）存在，
由（2）可知，
，即点
，
∵将点P向下平移
个单位得到点Q，
∴点Q(0,2)，
在Rt△AOQ中，
，
，则
，
取AQ的中点G，则有
，
∴△AOQ在旋转过程中，只需使AQ的中点G在坐标轴上即可满足GQ′＝OG，
如图所示，当点G在y轴正半轴上时，过点Q′作Q′I⊥x轴，垂足为I，
∵∠GOQ'＝∠GQ'O，
∵
，
∴∠GOQ'＝∠IQ'O，
∴∠IQ'O＝∠GQ'O，
∴设
，
∴
，
∴
，即点
，
同理可知，当点G在x轴正半轴上时，点
，
当点G在y轴负半轴上时，点
，
当点G在x轴负半轴上时，点
，
综上，点Q′的坐标为，，，．
