题目内容
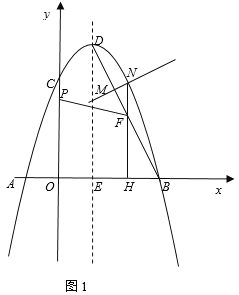
【题目】某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,并建立如下模型:设第t个月该原料药的月销售量为P(单位:吨),P与t之间存在如图所示的函数关系,其图像是函数P=![]() (0<t≤8)的图像与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=
(0<t≤8)的图像与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=![]()

(1)当8<t≤24时,求P关于t的函数表达式;
(2)设第t个月销售该原料药的月毛利润为w(单位:万元)
①求w关于t的函数表达式;
②未来两年内,当月销售量P为时,月毛利润为w达到最大.
【答案】(1)P=t+2;(2)①当0<t≤8时,w=240;当8<t≤12时,w=2t2+12t+16;当12<t≤24时,w=﹣t2+42t+88;②23
【解析】
(1)设8<t≤24时,P=kt+b,将A(8,10)、B(24,26)代入求解可得P=t+2;
(2)①分0<t≤8、8<t≤12和12<t≤24三种情况,根据月毛利润=月销量×每吨的毛利润可得函数解析式;
②当0<t≤8时,w的值始终是240;当8<t≤12时,w=2t2+12t+16=2(t+3)22,当t=12时,求得w值;当12<t≤24时,w=﹣t2+42t+88=﹣(t﹣21)2+529,根据二次函数的增减性求得当t=21时w的值,进而可得到结论.
解:(1)设8<t≤24时,P=kt+b,
将A(8,10)、B(24,26)代入,得:
![]()
解得:![]() ,
,
∴P=t+2;
(2)∵w=P·Q
∴①当0<t≤8时,w=(2t+8)×![]() =240;
=240;
当8<t≤12时,w=(2t+8) (t+2)=2t2+12t+16;
当12<t≤24时,w=(﹣t+44)(t+2)=﹣t2+42t+88;
②当0<t≤8时,w=240;
当8<t≤12时,w=2t2+12t+16=2(t+3)2﹣2,
∴8<t≤12时,w随t的增大而增大,
当t=12时,w取得最大值,最大值为448,
当12<t≤24时,w=﹣t2+42t+88=﹣(t﹣21)2+529,
当t=21时,w取得最大值529,
∵529>448>240
∴t=21时,w取得最大值
此时P=t+2=23

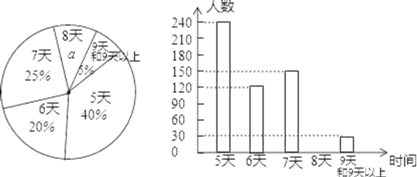
【题目】某校组织了2000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
成绩 | 频数 | 频率 |
| 20 |
|
| 16 | 0.08 |
|
| 0.15 |
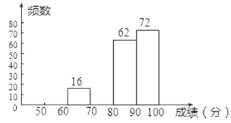
请你根据以上的信息,回答下列问题:
(1)![]() ,
,![]() ;
;
(2)在扇形统计图中,“成绩![]() 满足
满足![]() ”对应扇形的圆心角的度数是 ;
”对应扇形的圆心角的度数是 ;
(3)若将得分转化为等级,规定:![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() .这次全校参加竞赛的学生约有 人参赛成绩被评为“
.这次全校参加竞赛的学生约有 人参赛成绩被评为“![]() ”.
”.