题目内容
【题目】完成下面的证明:
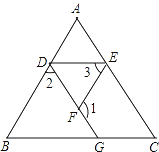
如图,已知∠1、∠2互为补角,且∠3=∠B,
求证:∠AED=∠ACB.
证明:∵∠1+∠2=180°,∠2+∠4=180°
∴∠1=∠4 (______)
∴AB∥EF(_______)
∴∠3=______(______)
又∠3=∠B
∴∠B=_______(_______)
∴DE∥BC (________)
∴∠AED=∠ACB (_______)

【答案】等式基本性质;内错角相等,两直线平行;∠ADE;两直线平行,内错角相等;∠ADE;等量代换;同位角相等,两直线平行;两直线平行,同位角相等.
【解析】
根据等式的基本性质、平行线的判定和性质以及等量代换进行推理填空即可.
证明:∵∠1+∠2=180°,∠2+∠4=180°,
∴∠1=∠4 (等式基本性质),
∴AB∥EF(内错角相等,两直线平行),
∴∠3=∠ADE(两直线平行,内错角相等),
又∠3=∠B,
∴∠B=∠ADE(等量代换),
∴DE∥BC(同位角相等,两直线平行),
∴∠AED=∠ACB (两直线平行,同位角相等),
故答案为:等式基本性质;内错角相等,两直线平行;∠ADE;两直线平行,内错角相等;∠ADE;等量代换;同位角相等,两直线平行;两直线平行,同位角相等.

练习册系列答案
相关题目