题目内容
若a，b，c是三角形三边的长，则代数式a2+b2-c2-2ab的值
- A.＞0
- B.＜0
- C.＞或等于0
- D.＜或等于0
B
分析：那所给代数式进行因式分解，根据各个因式的符号来确定整个代数式的符号．
解答：a2+b2-c2-2ab=（a-b）2-c2=（a-b+c）（a-b-c）=（a+c-b）[a-（b+c）]，
在三角形中，任意两边＞第三边，∴a+c-b＞0，
在三角形中，任意两边＜第三边，∴a-（b+c）＜0，
∴代数式a2+b2-c2-2ab的值是两个异号的数的积，是负数，即代数式的值＜0．
故选B．
点评：本题利用了三角形中三边的关系：在三角形中，任意两边之和＞第三边，任意两边之差＜第三边．
分析：那所给代数式进行因式分解，根据各个因式的符号来确定整个代数式的符号．
解答：a2+b2-c2-2ab=（a-b）2-c2=（a-b+c）（a-b-c）=（a+c-b）[a-（b+c）]，
在三角形中，任意两边＞第三边，∴a+c-b＞0，
在三角形中，任意两边＜第三边，∴a-（b+c）＜0，
∴代数式a2+b2-c2-2ab的值是两个异号的数的积，是负数，即代数式的值＜0．
故选B．
点评：本题利用了三角形中三边的关系：在三角形中，任意两边之和＞第三边，任意两边之差＜第三边．
练习册系列答案
相关题目
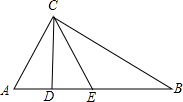如图，△ABC中，∠ACB=90°，CD、CE分别为斜边AB上的高和中线，若∠B=30°，则△ACE是