题目内容
(本题满分10分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.求证:

1.(1)D是BC的中点;2.(2)△BEC∽△ADC;3.(3)BC2=2AB·CE.
1.(1)证明:∵AB是⊙O的直径,∴∠ADB=90° ,
即AD是底边BC上的高. ………………………………………1分
又∵AB=AC,∴△ABC是等腰三角形,
∴D是BC的中点;………… ……………………………………………2分
2.(2)证明:∵∠CBE与∠CAD是同弧所对的圆周角,
∴ ∠CBE=∠CAD.……………………………………………2分
又∵ ∠BCE=∠ACD,
∴△BEC∽△ADC;…………………………………………………1分
3.(3)证明:由△BEC∽△ADC,知![]() ,
,
即CD·BC=AC·CE.…………………………………………………2分
∵D是BC的中点,∴CD=![]() BC.
BC.
又 ∵AB=AC,∴CD·BC=AC·CE=![]() BC ·BC=AB·CE
BC ·BC=AB·CE
即BC![]() =2AB·CE.………………………………………2分
=2AB·CE.………………………………………2分
解析:略

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目

 的图象的顶点为
的图象的顶点为 .二次函数
.二次函数 的图象与
的图象与 轴交于原点
轴交于原点 及另一点
及另一点 ,它的顶点
,它的顶点 在函数
在函数
 为菱形时,求函数
为菱形时,求函数 与支架
与支架 所在直线相交于水箱横断面
所在直线相交于水箱横断面 的圆心
的圆心 ,支架
,支架 垂直,
垂直, 厘米,
厘米,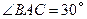 ,另一根辅助支架
,另一根辅助支架 厘米,
厘米, .
. 的长度.(结果保留三个有效数字,参考数据:
的长度.(结果保留三个有效数字,参考数据: )
)


