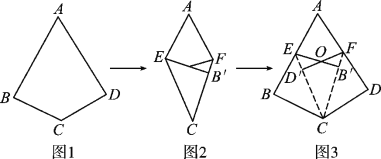
题目内容
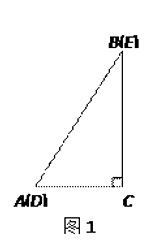
【题目】如图,在![]() 的
的![]() 边的异侧作
边的异侧作![]() ,并使
,并使![]() .点
.点![]() 在射线
在射线![]() 上.
上.
(1)如图,若![]() ,求证:
,求证:![]() ;
;
(2)若![]() ,试解决下面两个问题:
,试解决下面两个问题:
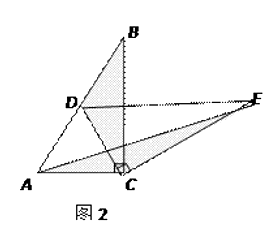
①如图2,![]() ,求
,求![]() 的度数;
的度数;
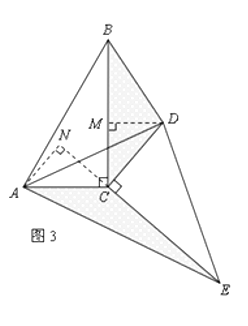
②如图3,若![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 的度数.
的度数.
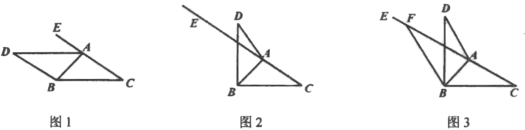
【答案】(1)证明过程见详解;(2)①35°;②117°.
【解析】
(1)根据平行线的性质,可以证得∠DAE=∠D,再通过等量代换得∠DAE=∠C,即可证明;
(2)①设CE与DB交于点G,利用三角形内角和为180°,分别在△CBG和△DAG中把∠CGB表示出来,均是关于∠C的关系式,即可求解;
②根据题设,可证明∠DBF=∠D=∠C,利用三角形内角和为180°,以及平角定义求得∠EFB=2∠C+90![]() ,又因为∠EFB=7∠DBF=7∠C,即可求得∠C=18°,而∠CBA=∠DBA,进而可以求得∠BAD的度数.
,又因为∠EFB=7∠DBF=7∠C,即可求得∠C=18°,而∠CBA=∠DBA,进而可以求得∠BAD的度数.
(1)证明:∵AC//BD
∴∠DAE=∠D
∵∠C=∠D
∴∠DAE=∠C.
∴AD//BC.
(2)①设CE与DB交于点G,如图:
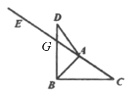
∵ BD⊥AC,∠C=∠D, ∠DAE=120![]()
∴∠CBG=90![]() ,
,
在△CBG中,∠CGB=180![]() -∠CBG -∠C =180
-∠CBG -∠C =180![]() -90
-90![]() -∠C,
-∠C,
在△DAG中,∠DGA=180![]() -∠D-∠DAE=180
-∠D-∠DAE=180![]() -∠C-20
-∠C-20![]() ,
,
而∠CGB=180![]() -∠DGA=180
-∠DGA=180![]() -(180
-(180![]() -∠C-20
-∠C-20![]() )=∠C+20
)=∠C+20![]() ,
,
即180![]() -90
-90![]() -∠C=∠C+20
-∠C=∠C+20![]() ,
,
解得∠C=35![]() .
.
故答案为35![]() .
.
②∵BF//AD,∠C=∠D,
∴∠DBF=∠D=∠C,
∵∠EFB=7∠DBF=7∠C,
又∵∠EFB=180![]() -∠CFB=180
-∠CFB=180![]() -(180
-(180![]() -∠C-90
-∠C-90![]() -∠DBF)=2∠C+90
-∠DBF)=2∠C+90![]() ,
,
即7∠C=2∠C+90![]() ,
,
解得∠C=∠D =18![]() ,
,
在△CBA和△DBA中,∠C=∠D,∠BAC=∠BAD,
∴∠CBA=∠DBA= ![]() .
.
∴∠BAD=180![]() -∠D-∠DBA=180
-∠D-∠DBA=180![]() -18
-18![]() -45
-45![]() =117
=117![]() .
.
故答案为117![]() .
.