题目内容
【题目】综合与探究
阅读理解:数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用较大数与较小数的差来表示.例如:
在数轴上,有理数3与1对应的两点之间的距离为![]() ;
;
在数轴上,有理数3与-2对应的两点之间的距离为![]() ;
;
在数轴上,有理数-3与-2对应的两点之间的距离为![]() .
.
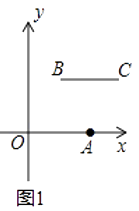
解决问题:如图所示,已知点![]() 表示的数为-3,点
表示的数为-3,点![]() 表示的数为-1,点
表示的数为-1,点![]() 表示的数为2.
表示的数为2.
![]()
(1)点![]() 和点
和点![]() 之间的距离为______.
之间的距离为______.
(2)若数轴上动点![]() 表示的数为
表示的数为![]() ,当
,当![]() 时,点
时,点![]() 和点
和点![]() 之间的距离可表示为______;当
之间的距离可表示为______;当![]() 时,点
时,点![]() 和点
和点![]() 之间的距离可表示为______.
之间的距离可表示为______.
(3)若数轴上动点![]() 表示的数为
表示的数为![]() ,点
,点![]() 在点
在点![]() 和点
和点![]() 之间,点
之间,点![]() 和点
和点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 和点
和点![]() 之间的距离表示为
之间的距离表示为![]() ,求
,求![]() (用含
(用含![]() 的代数式表示并进行化简)
的代数式表示并进行化简)
(4)若数轴上动点![]() 表示的数为-2,将点
表示的数为-2,将点![]() 向右移动19个单位长度,再向左移动23个单位长度终点为
向右移动19个单位长度,再向左移动23个单位长度终点为![]() ,那么
,那么![]() ,
,![]() 两点之间的距离是______.
两点之间的距离是______.
【答案】(1)5;(2)![]() ,
,![]() ;(3)12-x;(4)4
;(3)12-x;(4)4
【解析】
(1)用点C表示的数减去点A表示的数即可;
(2)当![]() 时,用点P表示的数减去点B表示的数即可;当
时,用点P表示的数减去点B表示的数即可;当![]() 时,用点B表示的数减去点P表示的数即可;
时,用点B表示的数减去点P表示的数即可;
(3)先表示出PA和PC,然后代入计算即可;
(4)先求出点Q表示的数,然后根据两点间距离的求法计算即可.
解:(1)2-(-3)=5;
(2)x-(-1)=![]() ;
;![]() ;
;
(3)∵PA=x-(-3)=x+3,PC=2-x,
∴![]()
![]()
![]() ;
;
(4)∵-2+19-23=-6,
∴![]() ,
,![]() 两点之间的距离是-2-(-6)=4.
两点之间的距离是-2-(-6)=4.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目