题目内容
如图所示,等边三角形ABC中,AB=2,点P是AB边上的任意一点(点P可以与点A重合,但不与点B重合),过点P作PE⊥BC,垂足为E,过E作EF⊥AC,垂足为F,过F作FQ⊥AQ,垂足为Q,设BP=x,AQ=y.
(1)写出y与x之间的函数关系式;
(2)当BP的长等于多少时,点P与点Q重合?

解:(1)因为△ABC为等边三角形,
所以∠A=∠B=∠C=60°,AB=BC=CA=2.
在△BEP中,因为PE⊥BE,∠B=60°,
所以∠BPE=30°,
而BP=x,所以BE=![]() x,EC=2-
x,EC=2-![]() x,
x,
在△CFE中,因为∠C=60°,EF⊥CF,
所以∠FEC=30°,所以FC=1-![]() x,
x,
同理在△FAQ中,可得AQ=![]() +
+![]() x,
x,
而AQ=y,所以y=![]() +
+![]() x(0<x≤2).
x(0<x≤2).
(2)当点P与点Q重合时,有AQ+BP=AB=2,
所以x+y=2,所以
解得x=![]() .
.
所以当BP的长为![]() 时,点P与点Q重合.
时,点P与点Q重合.

练习册系列答案
相关题目
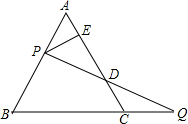 已知:如图所示,等边三角形ABC的边长为2,点P和Q分别从A和C两点同时出发,做匀速运动,且它们的速度相同.点P沿射线AB运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D,作PE⊥AC于E,当P和Q运动时,线段DE的长是否改变?证明你的结论.
已知:如图所示,等边三角形ABC的边长为2,点P和Q分别从A和C两点同时出发,做匀速运动,且它们的速度相同.点P沿射线AB运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D,作PE⊥AC于E,当P和Q运动时,线段DE的长是否改变?证明你的结论.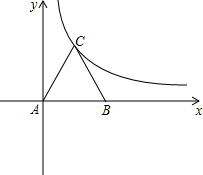 (2013•恩施州)如图所示,等边三角形ABC放置在平面直角坐标系中,已知A(0,0)、B(6,0),反比例函数的图象经过点C.
(2013•恩施州)如图所示,等边三角形ABC放置在平面直角坐标系中,已知A(0,0)、B(6,0),反比例函数的图象经过点C.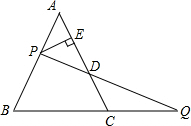 如图所示,等边三角形ABC的边长是6,点P在边AB上,点Q在BC的延长线上,且AP=CQ,设PQ与AC相交于点D.
如图所示,等边三角形ABC的边长是6,点P在边AB上,点Q在BC的延长线上,且AP=CQ,设PQ与AC相交于点D. 如图所示,等边三角形ABC的边长为a,分别以点A,B,C为圆心,以
如图所示,等边三角形ABC的边长为a,分别以点A,B,C为圆心,以
 如图所示,等边三角形ABC,点D为其内部一点,△BDC旋转后与△AEC重合,请判断△DCE的形状为
如图所示,等边三角形ABC,点D为其内部一点,△BDC旋转后与△AEC重合,请判断△DCE的形状为