题目内容
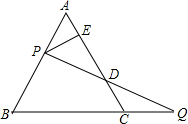 已知:如图所示,等边三角形ABC的边长为2,点P和Q分别从A和C两点同时出发,做匀速运动,且它们的速度相同.点P沿射线AB运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D,作PE⊥AC于E,当P和Q运动时,线段DE的长是否改变?证明你的结论.
已知:如图所示,等边三角形ABC的边长为2,点P和Q分别从A和C两点同时出发,做匀速运动,且它们的速度相同.点P沿射线AB运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D,作PE⊥AC于E,当P和Q运动时,线段DE的长是否改变?证明你的结论.
分析:作QF⊥AC,交直线AC的延长线于点F,易证△APE≌△CQF,可得AE=FC,PE=QF且PE∥QF,所以,四边形PEQF是平行四边形,即DE=
EF,等量代换得,DE=
AC,根据已知,即可得出DE的长为定值;
| 1 |
| 2 |
| 1 |
| 2 |
解答: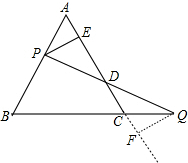 解:当点P、Q运动时,线段DE的长度不会改变.理由如下:
解:当点P、Q运动时,线段DE的长度不会改变.理由如下:
作QF⊥AC,交直线AC的延长线于点F,
又∵PE⊥AC于E,
∴∠CFQ=∠AEP=90°,
∵点P、Q做匀速运动且速度相同,
∴AP=CQ,
∵△ABC是等边三角形,
∴∠A=∠ACB=∠FCQ=60°,
∴在△APE和△CQF中
,
∴△APE≌△CQF,
∴AE=FC,PE=QF且PE∥QF,
∴四边形PEQF是平行四边形,
∴DE=
EF,
∵EC+CF=EC+AE=AC,
∴DE=
AC,
又∵等边△ABC的边长为2,
∴DE=1,
∴当点P、Q运动时,线段DE的长度不会改变.
 解:当点P、Q运动时,线段DE的长度不会改变.理由如下:
解:当点P、Q运动时,线段DE的长度不会改变.理由如下:作QF⊥AC,交直线AC的延长线于点F,
又∵PE⊥AC于E,
∴∠CFQ=∠AEP=90°,
∵点P、Q做匀速运动且速度相同,
∴AP=CQ,
∵△ABC是等边三角形,
∴∠A=∠ACB=∠FCQ=60°,
∴在△APE和△CQF中
|
∴△APE≌△CQF,
∴AE=FC,PE=QF且PE∥QF,
∴四边形PEQF是平行四边形,
∴DE=
| 1 |
| 2 |
∵EC+CF=EC+AE=AC,
∴DE=
| 1 |
| 2 |
又∵等边△ABC的边长为2,
∴DE=1,
∴当点P、Q运动时,线段DE的长度不会改变.
点评:本题主要考查了等边三角形的性质、全等三角形及平行四边形的判定与性质,平行四边形的判定及性质的运用,是解答本题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
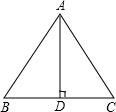 已知:如图所示,等边三角形ABC的边长是6cm.求:(1)高AD的长;(2)△ABC的面积S△ABC.
已知:如图所示,等边三角形ABC的边长是6cm.求:(1)高AD的长;(2)△ABC的面积S△ABC. 已知:如图所示,点C在线段AB上,分别以AC、BC为一边作为等边△ACM和等边△BCN,连接AN、BM.
已知:如图所示,点C在线段AB上,分别以AC、BC为一边作为等边△ACM和等边△BCN,连接AN、BM.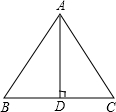 已知:如图所示,等边三角形ABC的边长是6cm.求:(1)高AD的长;(2)△ABC的面积S△ABC.
已知:如图所示,等边三角形ABC的边长是6cm.求:(1)高AD的长;(2)△ABC的面积S△ABC.