题目内容
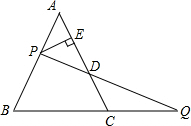 如图所示,等边三角形ABC的边长是6,点P在边AB上,点Q在BC的延长线上,且AP=CQ,设PQ与AC相交于点D.
如图所示,等边三角形ABC的边长是6,点P在边AB上,点Q在BC的延长线上,且AP=CQ,设PQ与AC相交于点D.(1)当∠DQC=30°时,求AP的长.
(2)作PE⊥AC于E,求证:DE=AE+CD.
分析:(1)求出∠QPB=90°,关键含30度角的直角三角形性质求出BP=
BQ,代入求出即可;
(2)求出AE=EF,证△PFD≌∠QCD,推出DF=CD,即可得出答案.
| 1 |
| 2 |
(2)求出AE=EF,证△PFD≌∠QCD,推出DF=CD,即可得出答案.
解答:(1)解:∵△ABC是等边三角形,
∴AB=BC=6,∠B=60°,
∵∠DQC=30°,
∴∠QPB=90°,
∴BP=
BQ,
设AP=CQ=a,
则6-a=
(6+a),
a=2,
即AP=2;
(2)
证明:过P作PF∥BC交AC于F,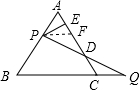
则∠APF=∠B,∠AFP=∠ACB,
∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°,
∴∠APF=∠AFP=∠A=60°,
∴AP=AF=PF,
∵AP=CQ,
∴PF=CQ,
∵PE⊥AC,AP=PF,
∴AE=EF,
∵PF∥BC,
∴∠PFD=?DCQ,
在△PFD和△QCD中
∴△PFD≌△QCD(AAS),
∴DF=CD,
∴DE=EF+DF=AE+CD.
∴AB=BC=6,∠B=60°,
∵∠DQC=30°,
∴∠QPB=90°,
∴BP=
| 1 |
| 2 |
设AP=CQ=a,
则6-a=
| 1 |
| 2 |
a=2,
即AP=2;
(2)
证明:过P作PF∥BC交AC于F,

则∠APF=∠B,∠AFP=∠ACB,
∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°,
∴∠APF=∠AFP=∠A=60°,
∴AP=AF=PF,
∵AP=CQ,
∴PF=CQ,
∵PE⊥AC,AP=PF,
∴AE=EF,
∵PF∥BC,
∴∠PFD=?DCQ,
在△PFD和△QCD中
|
∴△PFD≌△QCD(AAS),
∴DF=CD,
∴DE=EF+DF=AE+CD.
点评:本题考查了等边三角形性质,全等三角形的性质和判定,等腰三角形性质,平行线性质的应用,主要考查学生的推理能力.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
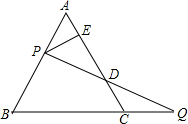 已知:如图所示,等边三角形ABC的边长为2,点P和Q分别从A和C两点同时出发,做匀速运动,且它们的速度相同.点P沿射线AB运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D,作PE⊥AC于E,当P和Q运动时,线段DE的长是否改变?证明你的结论.
已知:如图所示,等边三角形ABC的边长为2,点P和Q分别从A和C两点同时出发,做匀速运动,且它们的速度相同.点P沿射线AB运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D,作PE⊥AC于E,当P和Q运动时,线段DE的长是否改变?证明你的结论.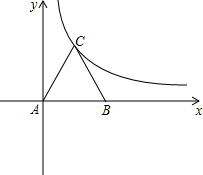 (2013•恩施州)如图所示,等边三角形ABC放置在平面直角坐标系中,已知A(0,0)、B(6,0),反比例函数的图象经过点C.
(2013•恩施州)如图所示,等边三角形ABC放置在平面直角坐标系中,已知A(0,0)、B(6,0),反比例函数的图象经过点C. 如图所示,等边三角形ABC的边长为a,分别以点A,B,C为圆心,以
如图所示,等边三角形ABC的边长为a,分别以点A,B,C为圆心,以
 如图所示,等边三角形ABC,点D为其内部一点,△BDC旋转后与△AEC重合,请判断△DCE的形状为
如图所示,等边三角形ABC,点D为其内部一点,△BDC旋转后与△AEC重合,请判断△DCE的形状为