题目内容
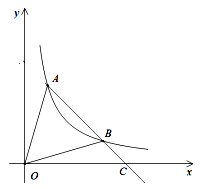
【题目】如图,A、B为反比例函数![]() 图像上的两点,A、B两点坐标分别为(
图像上的两点,A、B两点坐标分别为(![]() )、(
)、(![]() )(m<n),连接AB并延长交
)(m<n),连接AB并延长交![]() 轴于点C.
轴于点C.
(1)求![]() 的值;
的值;
(2)若B为AC的中点,求![]() 的值;
的值;
(3)过B点作OA的平行线交![]() 轴于(
轴于(![]() ,0),若
,0),若![]() 为整数,求
为整数,求![]() 值.
值.
【答案】(1)![]() 的值是5;
的值是5;
(2)![]() 的值为
的值为![]() ;
;
(3)![]() 值是
值是![]() 或
或![]() .
.
【解析】试题分析:(1) 把A、B两点坐标分别为(![]() )、(
)、(![]() )(m<n)代入反比例函数
)(m<n)代入反比例函数![]() 中,消去未知数k后,得到m与n的关系式:m=n(舍去),m+n=5;(2)设经过A、B两点的直线yAB=kx+b,把A、B两点坐标代入直线yAB中得,k=-1,b=4,即yAB=-x+5,则点C的坐标为(5,0),则A、B、C三点横坐标关系有:2(n-m)=5-m,再由(1)中m+n=5得,m=
中,消去未知数k后,得到m与n的关系式:m=n(舍去),m+n=5;(2)设经过A、B两点的直线yAB=kx+b,把A、B两点坐标代入直线yAB中得,k=-1,b=4,即yAB=-x+5,则点C的坐标为(5,0),则A、B、C三点横坐标关系有:2(n-m)=5-m,再由(1)中m+n=5得,m=![]() ,n=
,n=![]() ,则可求得k=
,则可求得k=![]() ;(3)由m+n=5,m<n得
;(3)由m+n=5,m<n得![]() ,所以m=1或m=2,再分情况讨论,求得xo的值即可;
,所以m=1或m=2,再分情况讨论,求得xo的值即可;
试题解析:
(1)把A、B两点坐标分别为(![]() )、(
)、(![]() )(m<n)代入反比例函数
)(m<n)代入反比例函数![]() 中得
中得

由①得,5m-m2=k……③
由②得,5n-n2=k……④
由④-③得,m-n=0或m+n-5=0
又∵(m<n)
∴m+n=5;
(2)设经过A、B两点的直线yAB=kx+b,
∵A、B两点坐标代入直线yAB中得
![]()
解得![]()
所以直线AB的解析式:yAB=-x+5
∴点C的坐标为(5,0)
∵B是AC的中点
∴2(n-m)=5-m
又∵m+n=5
∴m=![]() ,n=
,n=![]() ,
,
∴点A(![]() ,
, ![]() )、B(
)、B(![]() ,
, ![]() )
)
把点A(![]() ,
, ![]() )代入y=
)代入y=![]() 得:k=
得:k=![]() ;
;
(3)由m<n和(1)的结论,可知:![]() ,
,
又因为![]() 为整数,所以
为整数,所以![]() 或m=2
或m=2
由m=1时,则n=4,点A(1,4),B(4,1),
∴tan∠AOC=4:1,
∵过B点作OA的平行线交![]() 轴于(
轴于(![]() ,0),
,0),
∴tan∠AOC=1:(4-x0)=4:1
解得x0=![]() ;
;
由![]() ,类似地求得
,类似地求得![]() =
=![]() ;
;
所以过B点作OA的平行线交![]() 轴于(
轴于(![]() ,0),若
,0),若![]() 为整数,求
为整数,求![]() 值为
值为![]() 或
或![]() 。
。