题目内容
若△ABC的三边分别为a、b、c,且a2+b2+c2<6.证明:可以用一个单位圆覆盖△ABC.
证明:分两种情况:
①当△ABC为钝角三角形时,
不妨设c是最长边,此时,∠C>90°为钝角,
∴以c为直径的圆必然覆盖△ABC.
只需证明直径c<2即可.
根据柯西不等式:
a2+b2≥ (a+b)2>
(a+b)2> (c2),
(c2),
∴a2+b2+c2> (c2)+c2=
(c2)+c2= (c2)
(c2)
∴ (c2)<6 即:c2<4
(c2)<6 即:c2<4
∴c<2;
②当△ABC为锐角三角形时,
△ABC的外接圆必然可以覆盖它,
只需证明外接圆半径R<1;
根据正弦定理:
a=2RsinA,b=2RsinB,c=2RsinC,
即得:4(R2)[(sinA)2+(sinB)2+(sinC)2]<6,
应用三角恒等式:
(sinA)2+(sinB)2+(sinC)2=2+2cosAcosBcosC>2【用二倍角与和差化积易证】
∴8(R2)<4(R2)[(sinA)2+(sinB)2+(sinC)2]<6
∴R2<3/4<1,
∴R<1.
综上所述:用单位圆可以覆盖△ABC.
分析:只需要证明直径小于2或者半径小于1即可.根据已知条件,将三角形分为钝角三角形,锐角三角形两种情况分别证明.
点评:本题考查了三角形外接圆性质的运用.根据已知条件将三角形分类,运用特殊不等式解题.
①当△ABC为钝角三角形时,
不妨设c是最长边,此时,∠C>90°为钝角,
∴以c为直径的圆必然覆盖△ABC.
只需证明直径c<2即可.
根据柯西不等式:
a2+b2≥
 (a+b)2>
(a+b)2> (c2),
(c2),∴a2+b2+c2>
 (c2)+c2=
(c2)+c2= (c2)
(c2)∴
 (c2)<6 即:c2<4
(c2)<6 即:c2<4∴c<2;
②当△ABC为锐角三角形时,
△ABC的外接圆必然可以覆盖它,
只需证明外接圆半径R<1;
根据正弦定理:
a=2RsinA,b=2RsinB,c=2RsinC,
即得:4(R2)[(sinA)2+(sinB)2+(sinC)2]<6,
应用三角恒等式:
(sinA)2+(sinB)2+(sinC)2=2+2cosAcosBcosC>2【用二倍角与和差化积易证】
∴8(R2)<4(R2)[(sinA)2+(sinB)2+(sinC)2]<6
∴R2<3/4<1,
∴R<1.
综上所述:用单位圆可以覆盖△ABC.
分析:只需要证明直径小于2或者半径小于1即可.根据已知条件,将三角形分为钝角三角形,锐角三角形两种情况分别证明.
点评:本题考查了三角形外接圆性质的运用.根据已知条件将三角形分类,运用特殊不等式解题.

练习册系列答案
相关题目
若△ABC的三边分别为a,b,c,且满足|a-12|+(5-b)2+
≤0,则△ABC为( )
| sinC-1 |
| A、锐角三角形 |
| B、钝角三角形 |
| C、等腰直角三角形 |
| D、面积等于30的直角三角形 |
 三角形的内切圆
三角形的内切圆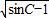 ≤0,则△ABC为( )
≤0,则△ABC为( )