题目内容
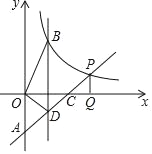
【题目】如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=3cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q两点同时出发。
(1)几秒钟后,P、Q间的距离等于4![]() cm?
cm?
(2)几秒种后,△BPQ的面积与四边形CQPA的面积相等?

【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)设时间为x秒,依题意得BP=xcm,AP=(6-x)cm,BQ=2xcm,在Rt△BPQ中利用勾股定理列方程求解;
(2)设a秒钟后,△BPQ的面积与四边形CQPA的面积相等,依题意得BP=acm,AP=(6-a)cm,BQ=2acm,然后表示出△BQP的面积和四边形CQPA的面积,列出方程,即可解出答案.
设x秒后,PQ=4![]() cm,则BQ=2x,BP=6-x,
cm,则BQ=2x,BP=6-x,
由题意得:BQ 2+BP 2=PQ 2,
∴(2x)2+(6x)2=(4![]() )2
)2
整理得:(5x-2)(x-2)=0,
解得:x1=![]() ,x2=2
,x2=2
∵BC=3cm,
∴x=2不合题意,舍去,
答:![]() 秒后PQ=4
秒后PQ=4![]() cm;
cm;
(2)设a秒钟后,△BPQ的面积与四边形CQPA的面积相等,则△BPQ的面积是△ABC的面积的一半,由题意得:
![]() ×2a×(6-a)=
×2a×(6-a)=![]() ×6×3,
×6×3,
解得:a=![]() ,
,
∵BC=3cm,
∴a=![]() 不合题意,舍去,
不合题意,舍去,
∴a=![]() .
.
答:![]() 秒钟后,△BPQ的面积与四边形CQPA的面积相等.
秒钟后,△BPQ的面积与四边形CQPA的面积相等.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案【题目】某水果批发市场,草莓的批发价格是每箱![]() 元,苹果的批发价格是每箱
元,苹果的批发价格是每箱![]() 元.
元.
(1)若李心批发草莓,苹果共![]() 箱,刚好花费
箱,刚好花费![]() 元,则他购买草莓、苹果各多少箱.
元,则他购买草莓、苹果各多少箱.
(2)李心有甲,乙两个店铺,每个店铺在同一时间段内都能售出草莓,苹果两种水果合计![]() 箱,并且每售出一箱草莓和苹果,甲店铺获毛利润分别为
箱,并且每售出一箱草莓和苹果,甲店铺获毛利润分别为![]() 元和
元和![]() 元,乙店铺获毛利润分别为
元,乙店铺获毛利润分别为![]() 元和
元和![]() 元.现在,李心要将批发购进的
元.现在,李心要将批发购进的![]() 箱草莓,
箱草莓,![]() 箱苹果分配给每个店铺各
箱苹果分配给每个店铺各![]() 箱.设分配给甲店草莓
箱.设分配给甲店草莓![]() 箱.
箱.
①根据信息填表:
草莓数量(箱) | 苹果数量(箱) | 合计(箱) | |
甲店 |
|
| |
乙店 |
|
②设李心获取的总毛利润为![]() 元,
元,
(1)求![]() 与
与![]() 的函数关系式:
的函数关系式:
(2)若在保证乙店铺获得毛利润不少于![]() 元的前提下,应怎样分配水果,使总毛利润
元的前提下,应怎样分配水果,使总毛利润![]() 最大,最大的总毛利润是多少元.
最大,最大的总毛利润是多少元.
【题目】为了解某社区居民的用电情况,随机对该社区10户居民进行调查,下表是这10户居民2018年4月份用电量的调查结果:
居民(户) | 1 | 2 | 3 | 4 |
月用电量(度) | 30 | 42 | 50 | 51 |
那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
A. 中位数是50度 B. 众数是51度
C. 方差是42度2 D. 平均数是46.8度