题目内容
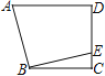
【题目】如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为___________.
【答案】10
【解析】
作BF⊥AD与F,就可以得出四边形BCDF是矩形,进而得出四边形BCDF是正方形,就有BC=BF=FD,证明△BCE≌△BFA就可以得出AF=CE,进而得出结论.
解:作BF⊥AD与F,
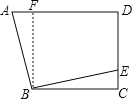
∴∠AFB=BFD=90°,
∵AD∥BC,
∴∠FBC=∠AFB=90°,
∵∠C=90°,
∴∠C=∠AFB=∠BFD=∠FBC=90°.
∴四边形BCDF是矩形.
∵BC=CD,
∴四边形BCDF是正方形,
∴BC=BF=FD.
∵EB⊥AB,
∴∠ABE=90°,
∴∠ABE=∠FBC,
∴∠ABE-∠FBE=∠FBC-∠FBE,
∴∠CBE=∠FBA.
在△BCE和△BFA中
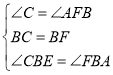
∴△BCE≌△BFA(ASA),
∴CE=FA.
∵CD=BC=8,DE=6,
∴DF=8,CE=2,
∴FA=2,
∴AD=8+2=10.
故答案为10.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目