题目内容
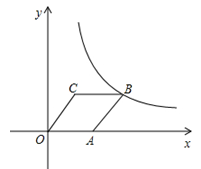
如图,直角三角形ABO放置在平面直角坐标系中,已知斜边OA在x轴正半轴上,且OA=4,AB=2,将该三角形绕着点O逆时针旋转120°后点B的对应点恰好落在一反比例函数图像上,则该反比例函数的解析式为 .

 .
.试题分析:在Rt△ABO中,根据勾股定理计算出OB=2
 ,利用正弦的定义得sin∠BOA=
,利用正弦的定义得sin∠BOA= ,则∠BOA=30°,设该三角形绕着点O逆时针旋转120°后点B的对应点为B′,根据旋转的性质得∠BOB′=120°,则OB′与x轴的负半轴的夹角为30°,且OB′=OB=2
,则∠BOA=30°,设该三角形绕着点O逆时针旋转120°后点B的对应点为B′,根据旋转的性质得∠BOB′=120°,则OB′与x轴的负半轴的夹角为30°,且OB′=OB=2 ,作B′H⊥x轴,在Rt△OB′H中,根据含30度的直角三角形三边的关系得B′H=
,作B′H⊥x轴,在Rt△OB′H中,根据含30度的直角三角形三边的关系得B′H=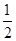 OB′=
OB′= ,OH=
,OH= B′H=3,所以B′点的坐标为(-3,
B′H=3,所以B′点的坐标为(-3, ),设点B′所落在的反比例函数解析式为y=
),设点B′所落在的反比例函数解析式为y= ,利用反比例函数图象上点的坐标特征得到k-3
,利用反比例函数图象上点的坐标特征得到k-3 ,从而得到该反比例函数的解析式为
,从而得到该反比例函数的解析式为 .
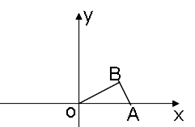
.在Rt△ABO中,OA=4,AB=2,
∴OB=
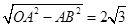 ,
,sin∠BOA=
 ,
,∴∠BOA=30°,
设该三角形绕着点O逆时针旋转120°后点B的对应点为B′,
∴OB′与x轴的负半轴的夹角为30°,OB′=OB=2
 ,
,作B′H⊥x轴,
在Rt△OB′H中,B′H=
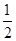 OB′=
OB′= ,OH=
,OH= B′H=3,
B′H=3,∴B′点的坐标为(-3,
 ),
),设点B′所落在的反比例函数解析式为
 ,
,∴k=-3×
 =-3
=-3
∴该反比例函数的解析式为
 .
.考点: 1.坐标与图形变化-旋转;2.反比例函数图象上点的坐标特征.

练习册系列答案
相关题目
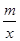 的图象经过点C.
的图象经过点C.

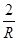 B.I=
B.I=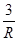
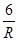 D.I=-
D.I=-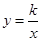 的图象经过点(-1,2),则这个函数的图象位于( )
的图象经过点(-1,2),则这个函数的图象位于( )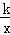 的图象上的一点,MA垂直y轴,垂足为A,△MAO的面积为2,则k的值为 .
的图象上的一点,MA垂直y轴,垂足为A,△MAO的面积为2,则k的值为 .
 图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为2,则k的值为( )
图象上一点,过点A作AB⊥y轴于点B,点P在x轴上,△ABP的面积为2,则k的值为( )
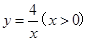 的图象上,斜边OA1,A1A2都在x轴上,则点A2的坐标是 .
的图象上,斜边OA1,A1A2都在x轴上,则点A2的坐标是 .
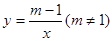 的图象在二、四象限,则m的取值范围 .
的图象在二、四象限,则m的取值范围 . (x>0)的图象经过顶点B,则k的值为 .
(x>0)的图象经过顶点B,则k的值为 .