题目内容
如图所示,已知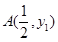 ,
, 为反比例函数
为反比例函数 图像上的两点,动点
图像上的两点,动点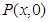 在
在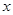 正半轴上运动,当线段
正半轴上运动,当线段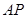 与线段
与线段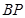 之差达到最大时,点
之差达到最大时,点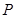 的坐标是( )
的坐标是( )

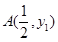 ,
, 为反比例函数
为反比例函数 图像上的两点,动点
图像上的两点,动点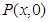 在
在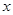 正半轴上运动,当线段
正半轴上运动,当线段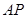 与线段
与线段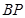 之差达到最大时,点
之差达到最大时,点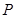 的坐标是( )
的坐标是( )
A.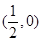 | B. | C.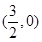 | D.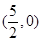 |
D
试题分析:先求出A、B的坐标,再根据待定系数法求出直线AB的解析式,根据三角形的三边关系定理得出在△ABP中,
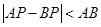 ,延长AB交x轴于P′,当P在P′点时,
,延长AB交x轴于P′,当P在P′点时,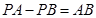 ,此时线段AP与线段BP之差达到最大,求出直线AB于x轴的交点坐标即可.
,此时线段AP与线段BP之差达到最大,求出直线AB于x轴的交点坐标即可.由
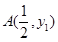 ,
, 为反比例函数
为反比例函数 图像上的两点,
图像上的两点,可得A(
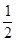 ,2),B(2,
,2),B(2,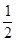 ),
),∵在△ABP中,
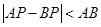 ,
,∴延长AB交x轴于P′,当P在P′点时,
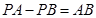 ,
,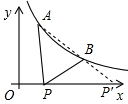
即此时线段AP与线段BP之差达到最大,
设直线AB的解析式是y=kx+b,
∵图象过点A(
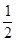 ,2),B(2,
,2),B(2,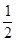 ),
),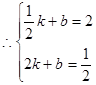 ,解得
,解得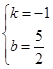 ,
,∴直线AB的解析式是
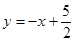 ,
,当
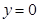 时,
时,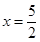 ,
,即P
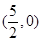 ,
,故选D.
点评:解答本题的关键是熟练掌握三角形的三边关系:三角形的任两边之和大于第三边;本题中确定P点的位置是突破口.

练习册系列答案
相关题目





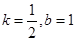
 与
与 轴的交点坐标是 ,与
轴的交点坐标是 ,与 轴的交点坐标是 .
轴的交点坐标是 .