题目内容
【题目】已知:等边△ABC的边长为2,点D为平面内一点,且BD=![]() AD=2
AD=2![]() ,则CD= .
,则CD= .
【答案】2或4
【解析】
试题分析:①根据等腰三角形的性质,可得DE的长,根据正弦函数,可得∠CAD的度数,根据等边三角形,可得CD的长;
②根据等腰三角形的性质,可得DE的长,根据正弦函数,可得∠EAD的度数,根据角的和差,可得A、C、D在同一条直线上,根据线段的和差,可得答案.
解:如图1:
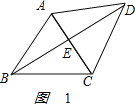
由BD=![]() AD=2
AD=2![]() ,得
,得
AD=AB=AC=2.
由等腰三角形的性质,得
DE=![]() .
.
sin∠DAE=![]() ,
,
∠DAE=60°,△ACD是等边三角形,
CD=AC=2;
如图2:
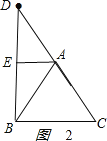 ,
,
由BD=![]() AD=2
AD=2![]() ,得
,得
AD=AB=AC=2.
由等边三角形的性质,得
DE=![]() ,∠DAE=∠BAE.
,∠DAE=∠BAE.
sin∠DAE=![]() ,
,
∠DAE=∠BAE=60°,
AD与AC在同一条直线上,
CD=AC=2;
CD=AD+AC=2+2=4.
故答案为:2或4.

练习册系列答案
相关题目