题目内容
下列图形都是由同样大小的黑点按一定的规律组成,其中第①个图形中一共有4个黑点,第②个图形中一共有9个黑点,第③个图形中一共有14个黑点,…,则第⑩个图形中黑点的个数是( )


| A、44 | B、48 | C、49 | D、54 |
考点:规律型:图形的变化类
专题:
分析:仔细观察图形的变化情况找到规律,利用规律解答即可.
解答:解:观察图形发现:
第一个图形有5×(1+1)-6=4个黑点;
第二个图形有5×(2+1)-6=9个黑点;
第三个图形有5×(3+1)-6=14个黑点;
第四个图形有5×(4+1)-6=19个黑点;
…
第一个图形有5×(n+1)-6=5n-1个黑点;
当n=10时,有50-1=49个黑点,
故选C.
第一个图形有5×(1+1)-6=4个黑点;
第二个图形有5×(2+1)-6=9个黑点;
第三个图形有5×(3+1)-6=14个黑点;
第四个图形有5×(4+1)-6=19个黑点;
…
第一个图形有5×(n+1)-6=5n-1个黑点;
当n=10时,有50-1=49个黑点,
故选C.
点评:本题考查了图形的变化类问题,解题的关键是仔细观察图形的变化规律,然后利用规律求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若有一等差数列,前九项和为54,且第一项、第四项、第七项的和为36,则此等差数列的公差为何?( )
| A、-6 | B、-3 | C、3 | D、6 |
在图1、图2、图3…中,菱形A1B1C1D1、菱形A2B2C2D2、菱形A3B3C3D3…都是由全等的小三角形拼成,菱形AnBnCnDn中有200个全等的小三角形,则n的值为( )
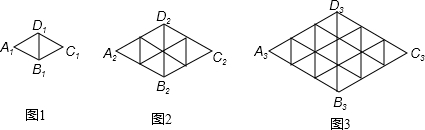

| A、10 | B、15 | C、20 | D、25 |
下列图形都是由同样大小的正方形按一定的规律组成,其中第(1)个图形中正方形的个数是1,第(2)个图形中正方形的个数是5,第(3)个图形中正方形的个数是14,第(4)个图形中正方形的个数是30,…,则第(7)个图形中正方形的个数是( )


| A、136 | B、140 | C、148 | D、156 |
用棋子摆出下列一组“口”字,按照这种方法摆下去,则摆第13个“口”字需用棋子( )


| A、48枚 | B、44枚 | C、52枚 | D、56枚 |
方程2x-1=3的解是( )
| A、-1 | ||
B、
| ||
| C、1 | ||
| D、2 |
下列图形中,不能通过折叠围成一个三棱柱的是( )
A、 | B、 | C、 | D、 |
