题目内容
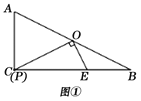
【题目】如图,将半径为2,圆心角为![]() 的扇形OAB绕点A逆时针旋转
的扇形OAB绕点A逆时针旋转![]() ,点O,B的对应点分别为
,点O,B的对应点分别为![]() ,
, ![]() ,连接
,连接![]() ,则图中阴影部分的面积是
,则图中阴影部分的面积是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】分析:连接OO′,BO′,根据旋转的性质得到∠OAO′=60°,推出△OAO′是等边三角形,得到∠AOO′=60°,推出△OO′B是等边三角形,得到∠AO′B=120°,得到∠O′B′B=∠O′BB′=30°,根据图形的面积公式即可得到结论.
详解:连接OO′,BO′,
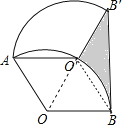
∵将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,
∴∠OAO′=60°,
∴△OAO′是等边三角形,
∴∠AOO′=60°,OO′=OA,
∴点O′中⊙O上,
∵∠AOB=120°,
∴∠O′OB=60°,
∴△OO′B是等边三角形,
∴∠AO′B=120°,
∵∠AO′B′=120°,
∴∠B′O′B=120°,
∴∠O′B′B=∠O′BB′=30°,
∴图中阴影部分的面积=S△B′O′B-(S扇形O′OB-S△OO′B)=![]() ×1×2
×1×2![]() -(
-(![]() -
-![]() ×2×
×2×![]() )=2
)=2![]() -
- ![]() .
.
故选C.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x) | 1 | 2 | 3 | 4 | … |
座位数(y) | 50 | 53 | 56 | 59 | … |
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.