��Ŀ����
����Ŀ����֪OC�ǡ�AOB�ڲ���һ�����ߣ�M��N�ֱ�ΪOA��OC�ϵĵ㣬�߶�OM��ONͬʱ�ֱ���30��/s��10��/s���ٶ��Ƶ�O��ʱ����ת������תʱ��Ϊt�룮
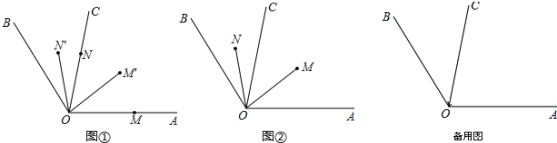
��1����ͼ�٣�����AOB��120������OM��ON��ʱ����ת��OM����ON������
����OM��ON��תʱ��tΪ2ʱ�����BON��+��COM��������������
����OM��ƽ�֡�AOC��ON��ƽ�֡�BOC�����M��ON����ֵ��
��2����ͼ�ڣ�����AOB��4��BOC��OM��ON�ֱ��ڡ�AOC����BOC�ڲ���תʱ��������COM���BON��������ϵ����˵�����ɣ�
��3������AOC��80����OM��ON����ת�Ĺ����У�����MON��20����t����������
���𰸡���1����40�㣻�ڡ�M��ON����60������2����COM��3��BON�����ɼ���������3��3���5�룮
��������
��1�����������AOM�䡢CON�䣬�ٱ�ʾ����BON�䡢��COM�䣬Ȼ����Ӳ����ݡ�AOB=120����㼴�ɵý⣻
�����ɽ�ƽ���������AOM��=��COM��=![]() ��AOC����BON��=��CON��=
��AOC����BON��=��CON��=![]() ��BOC���������COM��+��CON��=
��BOC���������COM��+��CON��=![]() ��AOB=
��AOB=![]() ��120��=60�㣬����M��ON��=60�㣻
��120��=60�㣬����M��ON��=60�㣻
��2������תʱ��Ϊt����ʾ����CON����AOM��Ȼ���з������õ���BON����COM�Ĺ�ϵ�����������ɵý⣻
��3������תʱ��Ϊt����ʾ����CON����AOM��Ȼ��õ���COM�����з������õ���MON�Ĺ�ϵ���������ɵý⣮
�⣺��1�������߶�OM��ON�ֱ���30��/s��10��/s���ٶ��Ƶ�O��ʱ����ת2s��
���AOM����2��30����60������CON����2��10����20����
���BON������BOC��20������COM������AOC��60����
���BON��+��COM������BOC��20��+��AOC��60������AOB��80����
�ߡ�AOB��120����
���BON��+��COM����120����80����40����
�ʴ�Ϊ��40����
�ڡ�OM��ƽ����AOC��ON��ƽ����BOC��
���AOM������COM����![]() ��AOC����BON������CON����
��AOC����BON������CON����![]() ��BOC��
��BOC��
���COM��+��CON����![]() ��AOC+
��AOC+![]() ��BOC��
��BOC��![]() ��AOB��
��AOB��![]() ��120����60����
��120����60����
����MON��60����
��2����COM��3��BON���������£�
����BOC��X������AOB��4X����AOC��3X��
����תt�����AOM��30t����CON��10t
���COM��3X��30t��3��X��10t������NOB��X��10t
���COM��3��BON��
��3������תt�����AOM��30t����CON��10t��
���COM��80����30t����NOC��10t��
�ɵ���MON����MOC+��CON��
�ɵã�|80����30t+10t|��20����
��ã�t��3���t��5�룬
�ʴ�Ϊ��3���5�룮