题目内容
【题目】随着夏季的来临,襄阳夜市大虾市场逐渐火爆,大虾供不应求.大虾养殖户莫小贝为了照顾更多的客户制定了如下销售方案:购买数量不大于50斤的部分,46元/斤;购买数量大于50斤但不大于m(120≤m≤200)斤的部分,60元/斤;购买数量大于m斤的部分,80元/斤.
(1)若胡胖子在莫小贝处购得大虾80斤,则他应付多少元钱?
(2)若胡胖子在莫小贝处购得大虾x斤,应付的钱数为y元,请列出y关于x的函数解析式;
(3)若胡胖子在莫小贝处购得大虾160斤,应付钱数y元的取值范围是8000≤y≤9000,试求m的取值范围.
【答案】(1)他应付4100元;(2)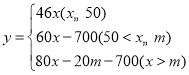 ;(3)155≤m<160.
;(3)155≤m<160.
【解析】
(1)根据题意列式计算;
(2)分三种情况:当x≤50时,当50<x≤m(120≤m≤200)时,当x>m时;分别列出三种情况下的函数解析式即可;
(3)当x=160时,由(2)知分两种情况讨论:当120≤m<160时和当m≥160时,列出关于m的不等式组,解之即可.
解:(1)由题意知:
若胡胖子在莫小贝处购得大虾80斤,则他应付的钱数为:50×46+(80﹣50)×60=4100(元)
答:若胡胖子在莫小贝处购得大虾80斤,则他应付4100元钱.
(2)当x≤50时,y=46x;
当50<x≤m(120≤m≤200)时,y=50×46+(x﹣50)×60=60x﹣700;
当x>m时,y=50×46+(m﹣50)×60+(x﹣m)×80=80x﹣20m﹣700;
∴y关于x的函数解析式为: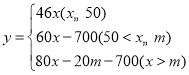 .
.
(3)当x=160时,由(2)知分两种情况讨论:
①当120≤m<160时,y=80x﹣20m﹣700
∴8000≤80×160﹣20m﹣700≤9000
解得:155≤m≤205
∴155≤m<160;
②当m≥160时,y=60x﹣700,此时60×160﹣700=9530>9000,不满足8000≤y≤9000,所以m≥160不成立;
综上所述:155≤m<160.

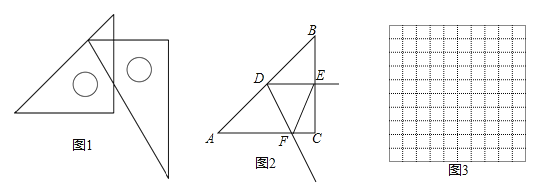
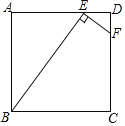
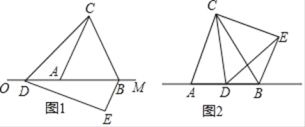
【题目】在数学活动课上,老师提出了一个问题:把一副三角尺如图摆放,直角三角尺的两条直角边分别垂直或平行,60°角的顶点在另一个三角尺的斜边上移动,在这个运动过程中,有哪些变量,能研究它们之间的关系吗?
小林选择了其中一对变量,根据学习函数的经验,对它们之间的关系进行了探究.
下面是小林的探究过程,请补充完整:
(1)画出几何图形,明确条件和探究对象;
如图2,在Rt△ABC中,∠C=90°,AC=BC=6cm,D是线段AB上一动点,射线DE⊥BC于点E,∠EDF=60°,射线DF与射线AC交于点F.设B,E两点间的距离为xcm,E,F两点间的距离为ycm.
(2)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 6.9 | 5.3 | 4.0 | 3.3 | 4.5 | 6 |
(说明:补全表格时相关数据保留一位小数)
(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(4)结合画出的函数图象,解决问题:当△DEF为等边三角形时,BE的长度约为 cm.