题目内容
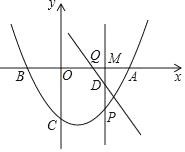
【题目】在学习完第十二章后,张老师让同学们独立完成课本56页第9题:“如图1,![]() ,
,![]() ,
,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.”
的长.”

(1)请你也独立完成这道题:
(2)待同学们完成这道题后,张老师又出示了一道题:
在课本原题其它条件不变的前提下,将![]() 所在直线旋转到
所在直线旋转到![]() 的外部(如图2),请你猜想
的外部(如图2),请你猜想![]() ,
,![]() ,
,![]() 三者之间的数量关系,直接写出结论:_______.(不需证明)
三者之间的数量关系,直接写出结论:_______.(不需证明)
(3)如图3,将(1)中的条件改为:在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 三点在同一条直线上,并且有∠BEC=∠ADC=∠BCA=
三点在同一条直线上,并且有∠BEC=∠ADC=∠BCA=![]() ,其中
,其中![]() 为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由:
为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)、(2)中的猜想还成立,证明见解析.
;(3)、(2)中的猜想还成立,证明见解析.
【解析】
(1)利用AAS定理证明△CEB≌△ADC,根据全等三角形的性质、结合图形解答.
(2)继续利用AAS定理证明△CEB≌△ADC,根据全等三角形的性质、结合图形解答.
(3)还是利用AAS定理证明△CEB≌△ADC,根据全等三角形的性质、结合图形解答.
(1)∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
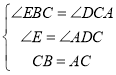 ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ;
;
(2)![]() ,
,
证明:∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°,
∴∠EBC+∠BCE=90°.
∵∠BCE+∠ACD=90°,
∴∠EBC=∠DCA.
在△CEB和△ADC中,
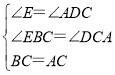 ,
,
∴△CEB≌△ADC(AAS),
∴BE=DC,CE=AD,
∴DE=CE+DE=AD+BE;
(3)、(2)中的猜想还成立,
证明:∵![]() ,
,![]() ,
,![]() ,
,
∴![]()
在![]() 和
和![]() 中,
中,
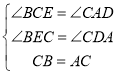 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.

【题目】为参加11月23日举行的丹东市“我爱诗词”中小学生诗词大赛决赛,某校每班选25名同学参加预选赛,成绩分别为A、B、C、D四个等级,其中相应等级的得分依次记为10分、9分、8分、7分,学校将八年级的一班和二班的成绩整理并绘制成如下统计图:

根据以上提供的信息解答下列问题
(1)请补全一班竞赛成绩统计图;
(2)请直接写出a、b、c、d的值;
班级 | 平均数(分) | 中位数(分) | 众数(分) |
一班 | a= | b= | 9 |
二班 | 8.76 | c= | d= |
(3)请从平均数和中位数两个方面对这两个班级的成绩进行分析.