题目内容
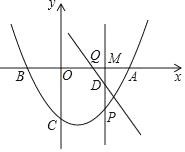
【题目】二次函数y=![]() +bx+c与一次函数y=kx﹣3的图象都经过x轴上的点A(4,0)和y轴上点C(0,﹣3).
+bx+c与一次函数y=kx﹣3的图象都经过x轴上的点A(4,0)和y轴上点C(0,﹣3).
(1)直接写出b,c,k的值,b= ,c= ,k= ;
(2)二次函数与x轴的另一个交点为B,点M(m,0)在线段AB上运动,过点M作x轴的垂线交直线AC于点D;交抛物线于点P.
①是否存在实数m,使△PCD为直角三角形.若存在、求出m的值;若不存在,请说明理由;
②当0<m<4时,过D作直线AC的垂线交x轴于点Q,求PD+DQ的最大值.
【答案】(1)﹣![]() ,﹣3;
,﹣3;![]() ;(2)①存在,m的值为2或﹣
;(2)①存在,m的值为2或﹣![]() ;②
;②![]() .
.
【解析】
(1)根据点A、B在二次函数![]() 的图象上,列方程组即可求出b、c的值,把点A代入y=kx﹣3求出k的值即可.(2)①由点M坐标为(m,0)可知点 D、P的坐标分别为D(m,
的图象上,列方程组即可求出b、c的值,把点A代入y=kx﹣3求出k的值即可.(2)①由点M坐标为(m,0)可知点 D、P的坐标分别为D(m,![]() m﹣3),P(m,
m﹣3),P(m,![]() m2﹣
m2﹣![]() m﹣3),当∠DPC=90°时,CP⊥PD,则
m﹣3),当∠DPC=90°时,CP⊥PD,则![]() m2﹣
m2﹣![]() m﹣3=﹣3,解方程得m=0(舍去)或m=2,当∠PCD=90°,CP⊥CD,
m﹣3=﹣3,解方程得m=0(舍去)或m=2,当∠PCD=90°,CP⊥CD,
直线PC交x轴于N,如图2,可证明△AMD∽△AOC,得OC2=ONOA,所以 ON=![]() 可知点N坐标为(﹣
可知点N坐标为(﹣![]() ,0),得直线CN的解析式为y=﹣
,0),得直线CN的解析式为y=﹣![]() x﹣3,列方程组求出P点坐标,即可得m的值.,②由可知OC=3,OA=4,AC=5,因为DM∥OC,所以△AMD∽△AOC,得
x﹣3,列方程组求出P点坐标,即可得m的值.,②由可知OC=3,OA=4,AC=5,因为DM∥OC,所以△AMD∽△AOC,得![]()
![]() ,AM=4-m,所以AD= -
,AM=4-m,所以AD= -![]() m+5,由DQ⊥AC,可证明△ADQ∽△AOC,所以
m+5,由DQ⊥AC,可证明△ADQ∽△AOC,所以![]() ,得DQ=﹣
,得DQ=﹣![]() m+
m+![]() ,因为DP=
,因为DP=![]() m﹣3﹣(
m﹣3﹣(![]() m2﹣
m2﹣![]() m﹣3),=﹣
m﹣3),=﹣![]() m2+
m2+![]() m,所以PQ+DQ=
m,所以PQ+DQ=![]() +
+![]() ,
,
当m=![]() 时,PQ+DQ有最大值
时,PQ+DQ有最大值![]() ,
,
(1)把A(4,0),C(0,﹣3)代入y=![]()
![]() +bx+c得
+bx+c得![]() 解得
解得  ,
,
∴抛物线解析式为y=![]()
![]() ﹣
﹣![]() x﹣3;
x﹣3;
把A(4,0)代入y=kx﹣3得4k﹣3=0,解得k=![]() ,
,
直线AC的解析式为y=![]() x﹣3;
x﹣3;
故答案为﹣![]() ,﹣3;
,﹣3;![]()
(2)①存在.
M(m,0),则D(m,![]() m﹣3),P(m,
m﹣3),P(m,![]() m2﹣
m2﹣![]() m﹣3),
m﹣3),
当∠DPC=90°时,CP⊥PD,则![]() m2﹣
m2﹣![]() m﹣3=﹣3,解得,m1=0(舍去),m2=2;
m﹣3=﹣3,解得,m1=0(舍去),m2=2;
当∠PCD=90°,CP⊥CD,
直线PC交x轴于N,如图2,
易得△CON∽△AOC,
∴OC2=ONOA,
∴ON=![]() ,则N(﹣
,则N(﹣![]() ,0),
,0),
易得直线CN的解析式为y=﹣![]() x﹣3,
x﹣3,
解方程组 得
得![]() 或
或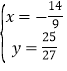 ,则P(﹣
,则P(﹣![]() ,﹣
,﹣![]() ),
),
综上所述,m的值为2或﹣![]() ;
;
②M(m,0),则D(m,![]() m﹣3),P(m,
m﹣3),P(m,![]() m2﹣
m2﹣![]() m﹣3),
m﹣3),
∵OC=3,OA=4,
∴AC=5,
∵DM∥OC,
∴△AMD∽△AOC,
∴![]()
![]() ,即
,即![]()
![]() ,解得AD=﹣
,解得AD=﹣![]() m+5,
m+5,
∵DQ⊥AC,
∴△ADQ∽△AOC,
∴![]() ,即
,即![]() =
=![]() ,解得DQ=﹣
,解得DQ=﹣![]() m+
m+![]() ,
,
而DP=![]() m﹣3﹣(
m﹣3﹣(![]() m2﹣
m2﹣![]() m﹣3)=﹣
m﹣3)=﹣![]() m2+
m2+![]() m,
m,
∴DP+DQ=﹣![]() m2+
m2+![]() m﹣
m﹣![]() m+
m+![]() =﹣
=﹣![]() m2+
m2+![]() m+
m+![]() =﹣
=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,
,
当m=![]() 时,PD+DQ有最大值为
时,PD+DQ有最大值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】如果一个多边形的各边都相等且各角也都相等,那么这样的多边形叫做正多边形,如正三角形就是等边三角形,正四边形就是正方形,如下图,就是一组正多边形,

(1)观察上面每个正多边形中的∠α,填写下表:
正多边形边数 | 3 | 4 | 5 | 6 | …… | n |
∠α的度数 | ______° | _____° | ______° | ______° | …… | _____° |
(2)根据规律,计算正八边形中的∠α的度数.
(3)是否存在正n边形使得∠α=21°?若存在,请求出n的值,若不存在,请说明理由.







