题目内容
【题目】有3张纸牌，分別是红桃3、红桃4和黑桃5（简称红3，红4，黑5）．把牌洗匀后甲先抽取一张，记下花色和数字后将牌放回，洗匀后乙再抽取一张．
（1）两次抽得纸牌均为红桃的概率；（请用“画树状图”或“列表”等方法写出分析过程）
（2）甲、乙两人做游戏，现有两种方案．A方案：若两次抽得花色相同则甲胜，否则乙胜．B方案：若两次抽得纸牌的数字和为奇数则甲胜，否则乙胜．请问甲选择哪种方案胜率更高？
【答案】（1）P(两次抽得纸牌均为红桃) =
；（2）甲选择A方案胜率更高，理由见解析.
【解析】分析: （1）首先根据题意列出表格，然后由表格即可求得所有等可能的结果；
（2）首先求得A方案与B方案中甲胜的概率，比较大小，即可确定甲选择哪种方案胜率更高．
详解:
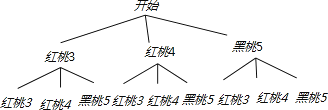
解：（1）树状图：
列表：
红桃3 | 红桃4 | 黑桃5 | |
红桃3 | （红3，红3） | （红3，红4） | （红3，黑5） |
红桃4 | （红4，红3） | （红4，红4） | （红4，黑5） |
黑桃5 | （黑5，红3） | （黑5，红4） | （黑5，黑5） |
∴一共有9种等可能的结果，其中符合要求的共4种，
∴P(两次抽得纸牌均为红桃)= 
．
（2）∵两次抽得相同花色的有5种，两次抽得数字和为奇数有4种，
A方案：P（甲胜）＝
，
B方案：P（甲胜）＝
，
∴甲选择A方案胜率更高．
点睛: 本题考查的是用列表法或画树状图法求概率．注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．注意概率＝所求情况数与总情况数之比．
练习册系列答案
星级口算天天练系列答案
相关题目
