��Ŀ����
����Ŀ�����ı���ABCD�У�AB��CD����BCD=90o��AB=AD=10cm��BC=8cm����P�ӵ�A������������ABCD������3cm/s���ٶ������˶�����Q�ӵ�D���������߶�
DC������2cm/s���ٶ������˶�. ��֪����ͬʱ��������һ���㵽���յ�ʱ����һ��Ҳֹͣ�˶������˶�ʱ��Ϊt��s��.
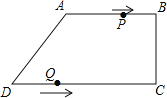
��1����CD�ij���
��2�����ı���PBQDΪƽ���ı���ʱ�����ı���PBQD���ܳ���
��3���ڵ�P��Q���˶������У��Ƿ����ijһʱ�̣�ʹ�á�BPQ�����Ϊ20cm2�������ڣ��������������������t��ֵ���������ڣ���˵������.
���𰸡���1��16cm��2����8+8![]() ��cm��3����t=
��cm��3����t=![]() ���
���![]() ��ʱ����BPQ�����Ϊ20cm2
��ʱ����BPQ�����Ϊ20cm2
�������������������1����A��AM��DC��M���ó�ƽ���ı���AMCB�����AM�����ݹ��ɶ������DM���ɣ�
��2������ƽ���ı��εĶԱ���ȵó����̣�������ɣ�
��3����Ϊ����������������⻭����������������ͼ�Σ����������ε�����ó����̣�������Ϸ�Χ�������ɣ�
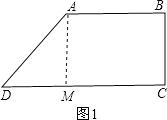
�����������1����ͼ1����A��AM��DC��M��
�����ı���ABCD�У�AB��CD����BCD=90�㣬
��AM��BC��
���ı���AMCB�Ǿ��Σ�
��AB=AD=10cm��BC=8cm��
��AM=BC=8cm��CM=AB=10cm��
��Rt��AMD�У��ɹ��ɶ����ã�DM=6cm��
CD=DM+CM=10cm+6cm=16cm��
��2����ͼ2�����ı���PBQD��ƽ���ı���ʱ��PB=DQ��
��10-3t=2t��
���t=2��
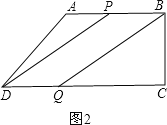
��ʱDQ=4��CQ=12��BQ=![]() =4
=4![]() ��
��
����C��PBQD=2��BQ+DQ��=8+8![]() ��
��
���ı���PBQD���ܳ��ǣ�8+8![]() ��cm��
��cm��
��3����P��AB��ʱ����ͼ3��
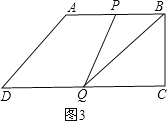
��0��t��![]() ��
��
S��BPQ=![]() BPBC=4��10-3t��=20��
BPBC=4��10-3t��=20��
���t=![]() ��
��
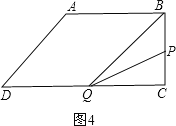
��P��BC��ʱ����ͼ4����![]() ��t��6��
��t��6��
S��BPQ=![]() BPCQ=
BPCQ=![]() ��3t-10����16-2t��=20����
��3t-10����16-2t��=20����
�˷���û��ʵ���⣻
��P��CD��ʱ��
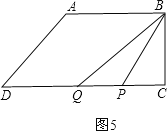
����P�ڵ�Q���Ҳ࣬��ͼ5����6��t��![]() ��
��
S��BPQ=![]() PQBC=4��34-5t��=20��
PQBC=4��34-5t��=20��
���t=![]() ��6���������⣬Ӧ��ȥ��
��6���������⣬Ӧ��ȥ��
��P��Q����࣬��ͼ6����![]() ��t��8��
��t��8��

S��BPQ=![]() PQBC=4��5t-34��=20��
PQBC=4��5t-34��=20��
���t=![]() ��������������t=
��������������t=![]() ���
���![]() ��ʱ����BPQ�����Ϊ20cm2��
��ʱ����BPQ�����Ϊ20cm2��

 ��У����ϵ�д�
��У����ϵ�д�