题目内容
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图像与函数
的图像与函数![]() (
(![]() )的图像相交于点
)的图像相交于点![]() ,并与
,并与![]() 轴交于点
轴交于点![]() .点
.点![]() 是线段
是线段![]() 上一点,
上一点,![]() 与
与![]() 的面积比为3:7.
的面积比为3:7.

(1)![]() _____,
_____,![]() _____.
_____.
(2)求点![]() 的坐标;
的坐标;
(3)若将![]() 绕点
绕点![]() 逆时针旋转,得到
逆时针旋转,得到![]() ,其中点
,其中点![]() 落在
落在![]() 轴负半轴上,判断点
轴负半轴上,判断点![]() 是否落在函数
是否落在函数![]() (
(![]() )的图像上,并说明理由.
)的图像上,并说明理由.
【答案】(1)-7,6;(2)(3,3),(3)点![]() 不在函数
不在函数![]() 的图象上,理由见解析.
的图象上,理由见解析.
【解析】
(1)将A(-1,7)代入y=-x+b可求出b的值;将A(-1,7)代入![]() 可求出k的值;
可求出k的值;
(2)过点D作DM⊥x轴,垂足为M,过点A作AN⊥x轴,垂足为N,由△ODC与△OAC的面积比为3:7,可推出![]() ,由点A的坐标可知AN=7,进一步求出DM=3,即为点D的纵坐标,把y=3代入y=-x+6中,可求出点D坐标;
,由点A的坐标可知AN=7,进一步求出DM=3,即为点D的纵坐标,把y=3代入y=-x+6中,可求出点D坐标;
(3)利用等积法和勾股定理计算旋转之后的点![]() 的坐标,代入判断是否满足反比例函数解析式即可得解.
的坐标,代入判断是否满足反比例函数解析式即可得解.
解:(1)将A(-1,7)代入y=-x+b,
得,7=1+b,
∴b=6,
将A(-1,7)代入![]() (x<0),
(x<0),
得,7=![]() ,
,
∴k=-7,
故答案为:-7,6;
(2)如图1,过点D作DM⊥x轴,垂足为M,过点A作AN⊥x轴,垂足为N,
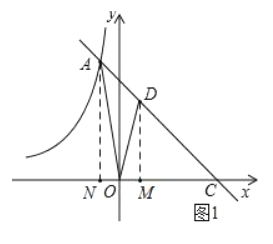
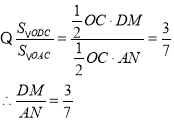 ,
,
又∵点A的坐标为(-1,7),
∴AN=7,
∴DM=3,即点D的纵坐标为3,
把y=3代入y=-x+6中,
得,x=3,
∴D(3,3);
(3)点![]() 不在函数
不在函数![]() 的图象上,理由如下:
的图象上,理由如下:
如图,过点![]() 作
作![]() ⊥
⊥![]() ,交
,交![]() 于H,
于H,

由直线AD的解析式y=-x+6,知点C(6,0),∴OC=6,![]() ,
,![]()
![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又点![]() 在第二象限,
在第二象限,
∴![]() 的坐标为(
的坐标为(![]() ,
,![]() ),
),
∵![]() ,
,
∴点![]() 不在函数
不在函数![]() 的图象上.
的图象上.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目