题目内容
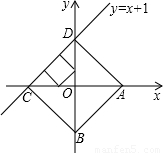
如图,正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;
(2)若某函数是反比例函数
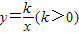 ,它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
,它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;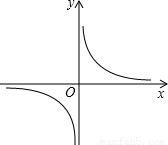
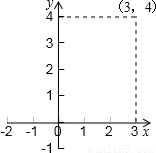
(3)若某函数是二次函数y=ax2+c(a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标______,写出符合题意的其中一条抛物线解析式______,并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数?______.(本小题只需直接写出答案)
【答案】分析:(1)设正方形ABCD的边长为a,当点A在x轴负半轴、点B在y轴正半轴上时,可知3a=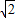 ,求出a,
,求出a,
(2)作DE、CF分别垂直于x、y轴,可知ADE≌△BAO≌△CBF,列出m的等式解出m,
(3)本问的抛物线解析式不止一个,求出其中一个.
解答:解:(1)∵正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.
当点A在x轴正半轴、点B在y轴负半轴上时,
∴AO=1,BO=1,
∴正方形ABCD的边长为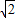 (1分)
(1分)
当点A在x轴负半轴、点B在y轴正半轴上时,
设正方形ABCD的边长为a,得3a=
∴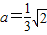 (1分)
(1分)
所以正方形边长为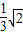 ;(1分)
;(1分)
(2)作DE、CF分别垂直于x、y轴,
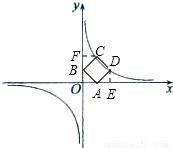
知△ADE≌△BAO≌△CBF(1分)
此时,m<2,DE=OA=BF=m
OB=CF=AE=2-m
∴OF=BF+OB=2
∴C点坐标为(2-m,2)(1分)
∴2m=2(2-m)
解得m=1(1分)
反比例函数的解析式为y= ;(1分)
;(1分)
(3)根据题意画出图形,如图所示:
过C作CF⊥x轴,垂足为F,过D作DE⊥CF,垂足为E,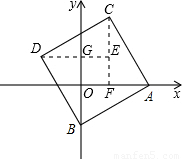
∴△CED≌△DGB≌△AOB≌△AFC,
∵C(3,4),即CF=4,OF=3,
∴EG=3,DE=4,故DG=DE-GE=DE-OF=4-3=1,
则D坐标为(-1,3);设过D与C的抛物线的解析式为:y=ax2+b,
把D和C的坐标代入得: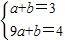 ,
,
解得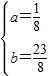 ,
,
∴满足题意的抛物线的解析式为y= x2+
x2+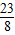 ;
;
同理可得D的坐标可以为:(7,-3);(-4,7);(4,1),(3分)
对应的抛物线分别为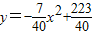 ;
;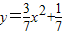 ;
; ,(1分)
,(1分)
所求的任何抛物线的伴侣正方形个数为偶数.(1分)
点评:本题主要考查二次函数的应用,此题开放性很强,应用二次函数解决实际问题比较简单.
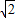 ,求出a,
,求出a,(2)作DE、CF分别垂直于x、y轴,可知ADE≌△BAO≌△CBF,列出m的等式解出m,
(3)本问的抛物线解析式不止一个,求出其中一个.
解答:解:(1)∵正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.
当点A在x轴正半轴、点B在y轴负半轴上时,
∴AO=1,BO=1,
∴正方形ABCD的边长为
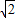 (1分)
(1分)当点A在x轴负半轴、点B在y轴正半轴上时,
设正方形ABCD的边长为a,得3a=

∴
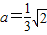 (1分)
(1分)所以正方形边长为
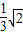 ;(1分)
;(1分)(2)作DE、CF分别垂直于x、y轴,

知△ADE≌△BAO≌△CBF(1分)
此时,m<2,DE=OA=BF=m
OB=CF=AE=2-m
∴OF=BF+OB=2
∴C点坐标为(2-m,2)(1分)
∴2m=2(2-m)
解得m=1(1分)
反比例函数的解析式为y=
 ;(1分)
;(1分)(3)根据题意画出图形,如图所示:
过C作CF⊥x轴,垂足为F,过D作DE⊥CF,垂足为E,

∴△CED≌△DGB≌△AOB≌△AFC,
∵C(3,4),即CF=4,OF=3,
∴EG=3,DE=4,故DG=DE-GE=DE-OF=4-3=1,
则D坐标为(-1,3);设过D与C的抛物线的解析式为:y=ax2+b,
把D和C的坐标代入得:
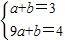 ,
,解得
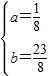 ,
,∴满足题意的抛物线的解析式为y=
 x2+
x2+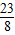 ;
;同理可得D的坐标可以为:(7,-3);(-4,7);(4,1),(3分)
对应的抛物线分别为
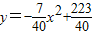 ;
;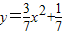 ;
; ,(1分)
,(1分)所求的任何抛物线的伴侣正方形个数为偶数.(1分)
点评:本题主要考查二次函数的应用,此题开放性很强,应用二次函数解决实际问题比较简单.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 19、如图:正方形ABCD,M是线段BC上一点,且不与B、C重合,AE⊥DM于E,CF⊥DM于F.求证:AE2+CF2=AD2.
19、如图:正方形ABCD,M是线段BC上一点,且不与B、C重合,AE⊥DM于E,CF⊥DM于F.求证:AE2+CF2=AD2. 如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE=
如图,正方形ABCD中,E点在BC上,AE平分∠BAC.若BE= 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( ) 17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是
17、如图,正方形ABCD的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与CD交于点F,与CB延长线交于点E,四边形AECF的面积是 如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.
如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE、DG.