题目内容
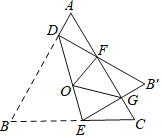
【题目】如图,矩形![]() 中,点
中,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,且
,且![]() 平分
平分![]() ,
,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,则线段
,则线段![]() 的长为______.
的长为______.
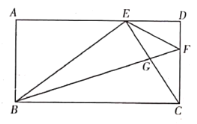
【答案】![]()
【解析】
延长AD、BF交于点H,作EQ⊥BH,根据AD∥BC,![]() 平分
平分![]() ,证明△EBH是等腰三角形,然后根据平行线分线段成比例定理求出
,证明△EBH是等腰三角形,然后根据平行线分线段成比例定理求出![]() ,设BF=4x,求出BQ=QH=3x,QF=x,根据等角的三角函数值相等可得
,设BF=4x,求出BQ=QH=3x,QF=x,根据等角的三角函数值相等可得![]() ,求出BC=6,然后利用勾股定理分别求出BF、EF、ED和CE,作CM⊥BF于M,利用等积法求得CM,根据△EQG∽△CMG列出比例式,得到
,求出BC=6,然后利用勾股定理分别求出BF、EF、ED和CE,作CM⊥BF于M,利用等积法求得CM,根据△EQG∽△CMG列出比例式,得到![]() ,求出
,求出![]() 即可解决问题.
即可解决问题.
解:延长AD、BF交于点H,作EQ⊥BH,
∵AD∥BC,![]() 平分
平分![]() ,
,
∴∠H=∠HBC,∠EBH=∠HBC,
∴∠H=∠EBH,
∴EB=EH,即△EBH是等腰三角形,
∵AD∥BC,
∴![]() ,
,
∴设BF=4x,则FH=2x,
∴BQ=QH=3x,QF=x,
∵![]() ,
,
∴EQ= QF=x,
∴tan∠H=![]() ,
,
∴tan∠FBC=![]() ,
,
∴BC=6,
∴BF=![]() ,
,
∴EQ=QF=![]() ,
,
∴EF=![]() ,
,
∴ED=![]() ,
,
∴CE=![]() ,
,
作CM⊥BF于M,则![]() ,
,
∴![]() ,
,
∵∠EQG=∠CMG,∠EGQ=∠CGM,
∴△EQG∽△CMG,
∴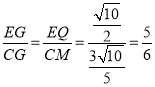 ,
,
∴![]() ,
,
∴![]() ,
,
故答案为:![]() .
.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目