题目内容
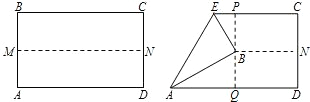
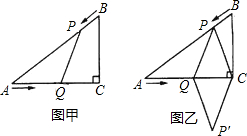
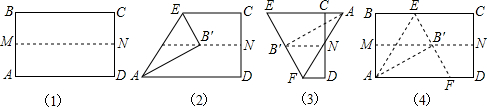
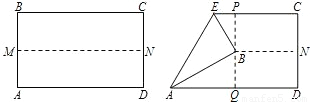
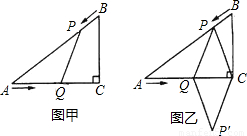
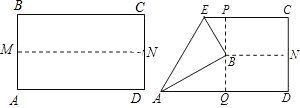如图，先把一矩形ABCD纸片对折，设折痕为MN，再把B点叠在折痕线上，得到△ABE．过B点折纸片使D点叠在直线AD上，得折痕PQ．（1）求证：△PBE∽△QAB；
（2）你认为△PBE和△BAE相似吗？如果相似，给出证明；若不相似，请说明理由．
分析：（1）△PBE和△QAB都是直角三角形，所以再证一对角相等即可．由∠ABE=90°得∠EBP+∠ABQ=90°，易证∠ABQ=∠PEB．得证．
（2）△PBE和△BAE都是直角三角形，利用（1）的结论，结合BP=BQ可证直角的两边对应成比例，得证．
（2）△PBE和△BAE都是直角三角形，利用（1）的结论，结合BP=BQ可证直角的两边对应成比例，得证．
解答：证明：（1）∵∠PBE+∠ABQ=90°，∠PBE+∠PEB=90°，
∴∠ABQ=∠PEB．
在△PBE与△QAB中，
∵∠ABQ=∠PEB，∠BPE=∠AQB=90°，
∴△PBE∽△QAB．
（2）△PBE和△BAE相似．
∵△PBE∽△QAB，
∴
=
．
∵BQ=PB，
∴
=
．
又∵∠EPB=∠EBA=90°，
∴△PBE∽△BAE．
∴∠ABQ=∠PEB．
在△PBE与△QAB中，
∵∠ABQ=∠PEB，∠BPE=∠AQB=90°，
∴△PBE∽△QAB．
（2）△PBE和△BAE相似．
∵△PBE∽△QAB，
∴
| BE |
| AB |
| PE |
| BQ |
∵BQ=PB，
∴
| BE |
| AB |
| PE |
| PB |
又∵∠EPB=∠EBA=90°，
∴△PBE∽△BAE．
点评：此题把折叠问题与相似三角形结合起来，有一定难度．
练习册系列答案
相关题目
