��Ŀ����
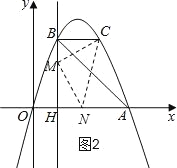
����Ŀ����ͼ��������y=ax2+bx��A��4��0����B��1��3�����㣬��C��B���������ߵĶԳ���Գƣ�����B��ֱ��BH��x�ᣬ��x���ڵ�H��

��1���������ߵı���ʽ��
��2��ֱ��д����C�����꣬�������ABC�������
��3����P����������һ���㣬��λ�ڵ������ޣ�����ABP�����Ϊ6ʱ�������P�����ꣻ
��4������M��ֱ��BH���˶�����N��x�����˶������Ե�C��M��NΪ�����������Ϊ����ֱ��������ʱ����ֱ��д����ʱ��CMN�������
���𰸡���1��y=��x2+4x����2����3��3����3����3����5����5������4��2.5��14.5��17��5
�������������������1�����ô���ϵ��������κ����ı���ʽ����2�����ݶ��κ����ĶԳ���x=2д����C������Ϊ��3��3�������������ʽ����ABC���������3����Ϊ��P����������һ���㣬��λ�ڵ������ޣ������P�����꣨m����m2+4m�������ò��ʾ��ABP���������ʽ�������m��ֵ��д����P�����ꣻ��4���ֱ��Ե�C��M��NΪֱ�Ƕ��������������ۣ�����ȫ�������κ��ɶ�����CM��CN�ij������������ʽ���м��㣮
�����������1���ѵ�A��4��0����B��1��3������������y=ax2+bx�У�
��![]() ��ã�
��ã� ![]() ��
��
�������߱���ʽΪ��y=��x2+4x��
��2����C��������3��3����
������B��������1��3����
��BC=2��
��S��ABC=![]() ��2��3=3��
��2��3=3��
��3����P����PD��BH��BH�ڵ�D��
���P��m����m2+4m����
�������⣬�ã�BH=AH=3��HD=m2��4m��PD=m��1��
��S��ABP=S��ABH+S�ı���HAPD��S��BPD��
6=![]() ��3��3+
��3��3+![]() ��3+m��1����m2��4m����
��3+m��1����m2��4m����![]() ��m��1����3+m2��4m����
��m��1����3+m2��4m����
��3m2��15m=0��
m1=0����ȥ����m2=5��
����P������5����5����
��4���Ե�C��M��NΪ�����������Ϊ����ֱ��������ʱ��������������ۣ�
���Ե�MΪֱ�Ƕ�����M��x���Ϸ�ʱ����ͼ2��CM=MN����CMN=90����
����CBM�ա�MHN��
��BC=MH=2��BM=HN=3��2=1��
��M��1��2����N��2��0����
�ɹ��ɶ����ã�MC=![]() ��
��
��S��CMN=![]() ��
��![]() ��
��![]() =
=![]() ��
��
���Ե�MΪֱ�Ƕ�����M��x���·�ʱ����ͼ3���������ߣ�������ͼ��ʾ����ֱ�������Σ�Rt��NEM��Rt��MDC��
��Rt��NEM��Rt��MDC��
��EM=CD=5��MD=ME=2��
�ɹ��ɶ����ã�CM=![]() =
=![]() ��
��
��S��CMN=![]() ��
��![]() ��
��![]() =
=![]() ��
��
���Ե�NΪֱ�Ƕ�����N��y�����ʱ����ͼ4��CN=MN����MNC=90�����������ߣ�
ͬ���ã�CN=![]() =
=![]() ��
��
��S��CMN=![]() ��
��![]() ��
��![]() =17��
=17��
���Ե�NΪֱ�Ƕ�����N��y���Ҳ�ʱ���������ߣ���ͼ5��ͬ���ã�CN=![]() =
=![]() ��
��
��S��CMN=![]() ��
��![]() ��
��![]() =5��
=5��
����CΪֱ�Ƕ���ʱ�����ܹ������������ĵ���ֱ�������Σ�
������������CMN������� ![]() ��
��![]() ��17��5��
��17��5��